Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 96

96- Demonstre que o circuito R L C em paralelo mostrado na Figura 16.105 é estável.

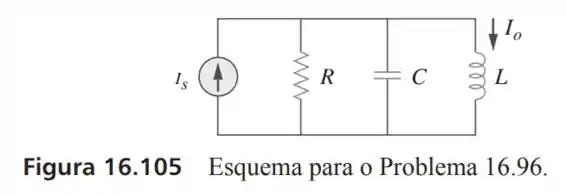
Passo 1

Supondo que a corrente no resistor vale I R , a corrente no capacitor vale I C e a corrente no indutor é I L = I o e que todos os componentes (por estarem em paralelo) estão sobre a mesma tensão V o então teremos:

I s = I R + I C + I L

O que será:

I S = V o R + C d V o d t + 1 L ∫ v t d t

I s = V o R + C s V o + V o L s

I s = V o 1 R + C s + 1 L s

V o = I s 1 R + C s + 1 L s = I s L s + R L C s + R R L s = R L s I s R L C s 2 + L s + R

Passo 2

Só que nós temos um circuito onde a entrada é a fonte de corrente I s e a saída a corrente I o que é a corrente que passa no indutor, então a função de transferência deveria ser algo da forma:

H s = I o I s

Então por isso a tensão no indutor será:

I o = V o L s → V o = L s I o

Substiutindo temos:

L s I o = R L s I s R L C s 2 + L s + R

I o I s = R R L C s 2 + L s + R

Dividindo tudo por R L C temos:

I o I s = 1 L C s 2 + 1 R C s + 1 L C

Passo 3

Para ser estável o sistema os pólos (as raízes do denominador ) tem que ser negativas.Então fazendo Bháskara no denominador temos:

r 1 ; r 2 = - 1 R C ± 1 R C 2 - 4 L C 2

( r 1 ; r 2 = - 1 2 R C ± 1 4 R 2 C 2 - 1 L C

Com certeza:

1 4 R 2 C 2 < 1 2 R C

Então se 1 L C > 1 4 R 2 C 2   o resultado da raíz será complexa, de modo que - 1 2 R C levará o sistema a estabilidade, e se 1 / L C for menor que 1 4 R 2 C 2   a raiz desse termo será menor que 1 / 2 R C fazendo com as duas raízes sejam negativas de qualquer maneira, logo o sistema é sim estável. Já que os valores de R , L e C são negativos.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro