Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 5.Problemas - Ex. 32

O amp op no circuito da Figura P5.32 é ideal.

a) Desenhe um gráfico de v o   v e r s u s   a   q u a n d o   R f   =   4 R 1   e   v g   =   2   V . Use incrementos de 0,1 e observe, por hipótese, que 0 ≤   a   ≤ 1,0 .  

b) Escreva uma equação para a reta que você obteve no gráfico de (a). Qual é a relação entre a inclinação da reta e sua interseção com o eixo v o e os valores de v g e a razão R f   / R 1 ?

c) Usando os resultados de (b), escolha valores de v g e da razão R f   / R 1 tais que v o   =   - 6 a   +   4 .

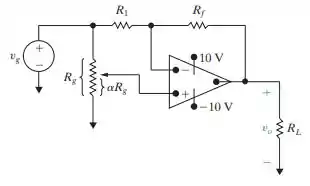
Passo 1

E ai meus queridos? Tudo certinho?

Então vem comigo que no caminho eu explicooo

  1. Iremos iniciar aplicando a divisão de tensão para encontrar a tensão no terminal não inversor

    2. v p = α R g α R g + R g - α R g ( v g )

    Devido ao conceito de solo virtual

    v n = v p

    = α v g

    Aplicando a lei das correntes de Kirchhoff no terminal inversor

    v n - v g R 1 + v n - v o R f = 0

    v n - v g R f + v n - v o R 1 R 1 R f = 0

    v n - v g R f + v n - v o R 1 = 0

    v n - v g R f = - v n - v o R 1

    Por outras simplificações

    v n - v g R f R 1 = - v n + v o

    v o = v n - v g R f R 1 + v n

    v o = v n R f R 1 - v g R f R 1 + v n

    v o = v n 1 + R f R 1 - R f R 1 v g

    Passo 2

    Calcularemos a tensão de saída para o amplificador somador

    v o = 1 + R f R g α v g - R f R 1 v g

    = 1 + R f R g α v g - 4 v g

    = α v g - v g 4 - α v g

    = α - 1 4 v g + α v g

    = α - 1 4 + α v g

    = 5 α - 4 v g

    = 5 α - 4 2

    = 10 α - 8

    Calculando a tensão de saída para α = 0

    v o = 10 α - 8

    = 10 0 - 8

    = - 8   V

    Calculando a tensão de saída para α = 0.1

    v o = 10 α - 8

    = 10 0.1 - 8

    = 1 - 8   V

    = - 7   V

    Calculando a tensão de saída para α = 0.2

    v o = 10 α - 8

    = 10 0.2 - 8

    = 2 - 8   V

    = - 6   V

    Passo 3

    Calculando a tensão de saída para α = 0.3

    v o = 10 α - 8

    = 10 0.3 - 8

    = 3 - 8   V

    = - 5   V

    Calculando a tensão de saída para α = 0.4

    v o = 10 α - 8

    = 10 0.4 - 8

    = 4 - 8   V

    = - 4   V

    Calculando a tensão de saída para α = 0.5

    v o = 10 α - 8

    = 10 0.5 - 8

    = 5 - 8   V

    = - 3   V

    Calculando a tensão de saída para α = 0.6

    v o = 10 α - 8

    = 10 0.6 - 8

    = 6 - 8   V

    = - 2   V

    Passo 4

    Calculando a tensão de saída para α = 0.7

    v o = 10 α - 8

    = 10 0.7 - 8

    = 7 - 8   V

    = - 1   V

    Calculando a tensão de saída para α = 0.8

    v o = 10 α - 8

    = 10 0.8 - 8

    = 8 - 8   V

    = 0   V

    Calculando a tensão de saída para α = 0.9

    v o = 10 α - 8

    = 10 0.9 - 8

    = 9 - 8   V

    = 1   V

    Calculando a tensão de saída para α = 1

    v o = 10 α - 8

    = 10 1 - 8

    = 10 - 8   V

    = 2   V

    Passo 5

    O gráfico para v o versus α são mostrados na Figura abaixo

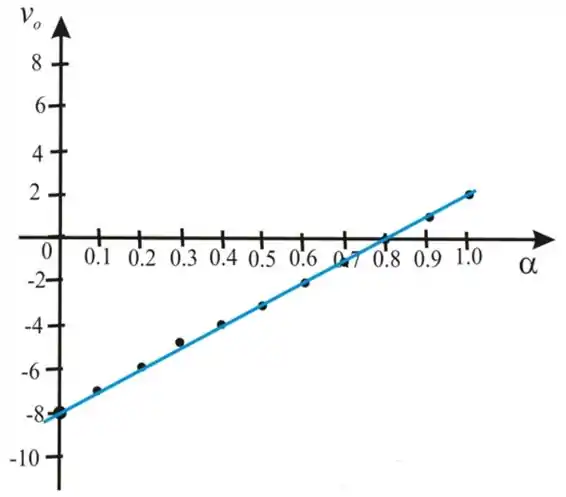
    Passo 6

  2. Reorganizando a expressão para v o da parte (a) dá

    3. v o = 1 + R f R g α v g - R f R 1 v g                 ( 1 )

    A equação da linha reta á dado como y = m x + c                       ( 2 )

    Equacione os coeficientes das equações (1) e (2)

    m = R f R 1 + 1 v g

    c = - R f R 1 v g

    Portanto, a inclinação é m e a interceptação é c

    Passo 7

  3. Substituindo o valor da inclinação na equação de (b)

- 6 = R f R 1 + 1 v g             ( 3 )

Substitua o valor de interceptação na equação de (b)

4 = - R f R 1 v g

- 4 v g = R f R 1                             ( 4 )

Substituindo a equação (4) em (3)

- 6 = - 4 v g + 1 v g

- 6 = - 4 v g v g + v g

- 6 = - 4 + v g

v g = - 2   V

Portanto, o valor da tensão da fonte é -2 V.

Substitua a tensão da fonte na fonte na equação para encontrar a relação de resistência

- 4 v g = R f R 1

- 4 - 2 = R f R 1

R f R 1 = 2

Portanto, a razão de resistência é 2.

Resposta

  1. Vide o passo a passo.
  2. Portanto, a inclinação é m e a interceptação é c.
  3. Portanto, o valor da tensão da fonte é -2 V.

Portanto, a razão de resistência é 2.

Exercícios de Livros Relacionados

a) Se o erro percentual for definido como % e r r o = v a l o ra p r o x i m a d ov a l o rr e a l - 1 × 100 , mostre que o erro percentual na aproximação de v o no Problema % e r r o = ∆ R RR + R f R
Suponha que o valor da resistência dos extensômetros na ponte da Figura 5.21 seja 120Ω ± 1 % . A fonte de alimentação do amp op fornece ± 15 V e a tensão de referência, vref, é o valor positivo da fon
O amp op no circuito amplificador não inversor da Figura P5.48 tem uma resistência de entrada de 560 kV, uma resistência de saída de 8 kV e um ganho de malha aberta de 50.000. Suponha que o amp op est
O amp op no circuito amplificador não inversor da Figura P5.48 tem uma resistência de entrada de 560 kV, uma resistência de saída de 8 kV e um ganho de malha aberta de 50.000. Suponha que o amp op est
O amp op no circuito amplificador não inversor da Figura P5.48 tem uma resistência de entrada de 560 kV, uma resistência de saída de 8 kV e um ganho de malha aberta de 50.000. Suponha que o amp op est