Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 5.Problemas - Ex. 25
a) Use o princípio da superposição para deduzir a Equação 5.22.
b) Deduza as equações 5.23 e 5.24.
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
Consultando a figura 5.15 para ver o circuito no livro
Observe que a tensão no terminal inversor (-) do amplificador operacional é , em relação ao terminal de aterramento e a tensão no terminal não inversor (+) do amplificador operacional é em relação ao terminal de aterramento.
Um op-amp ideal não consome corrente em seus terminais.
- Princípio da superposição:
- O fator de escala aplicado é . E o fator de escala aplicado em é
Ele afirma que a tensão através de um elemento ou corrente através de um elemento em um circuito produzido por múltiplas fontes é igual à soma das tensões através do elemento ou da soma das correntes através do elemento obtido quando cada fonte atua sozinho no circuito.
Uma fonte de tensão pode ser zerada substituindo – a por um curto – circuito, enquanto uma fonte de corrente por um circuito aberto.
Passo 2
Vamos definir a fonte de tensão para zero. Substituindo por um curto – circuito conforme mostrado na figura a seguir, iremos determinar a tensão de saída quando a fonte de tensão está agindo sozinha
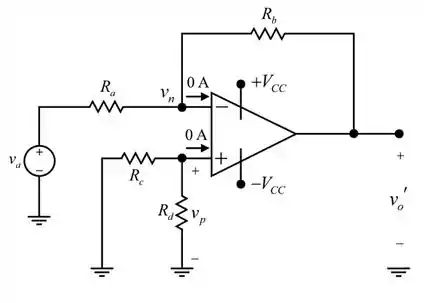
Passo 3
Aplicando a lei das correntes de Kirchhoff no nó inversor do circuito mostrado na figura anterior
Onde é a corrente que flui para o terminal negativo do amplificador operacional
Devido ao aterramento virtual no amplificador operacional, a tensão em inversores e não inversores terminais são iguais. Por isso
Como nenhuma corrente flui para os terminais do amplificador operacional, nenhuma corrente flui através das resistências
Logo
Passo 4
Substituindo 0 por na equação (1)
Sendo assim, a tensão de saída quando a fonte de tensão agindo sozinha é
Definindo a fonte de tensão para zero. Substituindo por um curto – circuito conforme mostrado na figura a seguir.
Determinaremos a tensão de saída quando a fonte de tensão está agindo sozinha
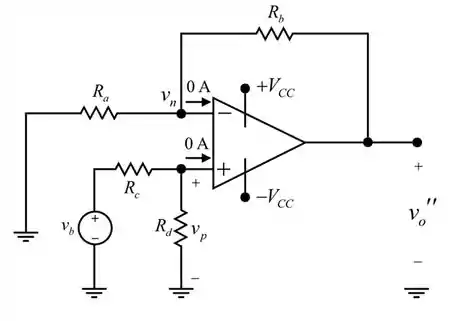
Passo 5
Aplicando a lei das correntes de Kirchhoff no nó não inversor do circuito mostrado na primeira figura, temos
Devido ao aterramento virtual no amplificador operacional, a tensão em inversores e não inversores nos terminais são iguais. Portanto
Aplicando a regra de divisão de tensão através da resistência no circuito mostrado na segunda imagem.
Passo 6
Substituindo em , temos
Portanto, a tensão de saída quando a fonte de tensão que está agindo sozinha é
Passo 7
Aplicando o principio da superposição .
Sendo assim, a equação 5.22 no livro é derivado usando o principio da sobreposição.
Passo 8
Derivaremos a condição tal que ambos os fatores de escala se tornem iguais
Simplificando ainda amis
Portanto
Sendo assim, a equação 5.23 no livro didático é derivado
Passo 2
Contudo
Derivaremos a expressão para tal que ambos os fatores de escala se tornem iguais
Parte (a)
Portanto, a equação 5.24 do livro didático é derivado.
Resposta
- Sendo assim, a equação 5.22 no livro é derivado usando o principio da sobreposição.
- Sendo assim, a equação 5.23 no livro didático é derivado.
Portanto, a equação 5.24 do livro didático é derivado.