Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 19.Problemas - Ex. 98

Um amplificador de dois estágios indicado na Figura 19.134 contém dois estágios idênticos com

h = 2   k Ω 0,004 200 500   μ S

Se Z L = 20   k Ω determine o valor necessário de V s para gerar V 0 = 16   V .

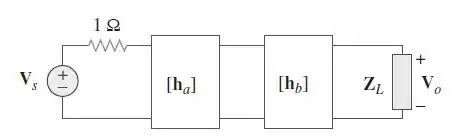
Passo 1

Galera, como os parâmetros de transmissão para circuitos de duas portas conectados em cascata são os produtos dos parâmetros de transmissão para parâmetros individuais, nós devemos converter os parâmetros h dos amplificadores a e b para os parâmetros de transmissão correspondentes. Daí, nós calculamos os parâmetros de transmissão para o circuito.

Usando a tabela 19.1 nós podemos obter a matriz de transmissão para um amplificador de estágio único:

T a = [ T b ] = ∆ h h 21 - h 11 h 21 - h 22 h 21 - 1 h 21 = - 0,001 - 10   Ω - 2,5 × 10 -   S - 0 , 005

onde ∆ h = 2000 × 500 × 10 - 6 - 200 × 0,004 = 0,2

Os parâmetros de transmissão para o circuito:

T = - 0,001 - 10   Ω - 2,5 × 10 -   S - 0,005 - 0,001 - 10   Ω - 2,5 × 10 -   S - 0,005 = 2,6 × 10 - 5 0,06   Ω 1,5 × 10 - 8 S 5 × 10 - 5

Passo 2

O circuito equivalente é mostrado na figura abaixo.

V 1 = A V 2 - B I 2

I 1 = C V 2 - D I 2

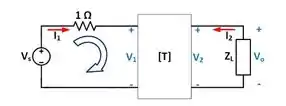
Ou,

V 1 = A V 0 - B I 2 … ( 1 )

I 1 = C V 0 - D I 2 … ( 2 )

Aplicando a lei das malhas na malha da esquerda, temos:

V S = I 1 + V 1 … 3

V 0 = - I 2 Z L

I 2 = - V 0 Z L … ( 4 )

Somando as equações ( 1 ) e ( 2 ) ,

V 1 + I 1 = A + C V 0 - B + D I 2 … 5

Substituindo as equações ( 3 ) e ( 4 ) na equação ( 5 ) :

V s = A + C V 0 - B + D - V 0 Z L

V s = A + C + B + D Z L V 0

Logo,

V s = 2,6 × 10 - 5 + 1,5 × 10 - 8 + 0,06 + 5 × 10 - 5 20000 × 16

V s = 4,6428 × 10 - 4   V

Resposta

A tensão V s é igual a:

V s = 4,6428 × 10 - 4   V

Ver Outros Exercícios desse livro