Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 19.Problemas - Ex. 95

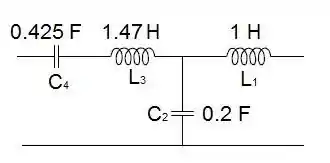
Concretize um circuito em cascata L C tal que

y 22 = s 3 + 5 s s 4 + 10 s 2 + 8

Passo 1

Pessoal, vamos dizer que Z A é a impedância do circuito.

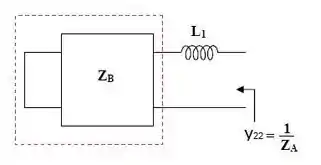
Assim,

Z A = 1 y 22

Z A = s 4 + 10 s 2 + 8 s 3 + 5 s

Para determinar L 1 , nós devemos simplificar essa fração usando frações parciais:

Z A = s 4 + 5 s 2 + 5 s 2 + 8 s 3 + 5 s

Z A = s s 3 + 5 s + 5 s 2 + 8 s 3 + 5 s

Z A = s s 3 + 5 s s 3 + 5 s + 5 s 2 + 8 s 3 + 5 s

Z A = s + 5 s 2 + 8 s 3 + 5 s

Z A = s L 1 + Z B

Assim,

L 1 = 1   H ,     Z B = 5 s 2 + 8 s 3 + 5 s

Passo 2

A impedância Z B corresponde a admitância Y B :

Y B = 1 Z B = s 3 + 5 s 5 s 2 + 8

Para determinar o valor de C 2 nós devemos simplificar a fração através da divisão de polinômios:

Y B = 0,2 s + 3,4 s 5 s 2 + 8 = s C 2 + Y C

Assim,

C 2 = 0,2   F ,     Y C = 3,4 s 5 s 2 + 8

A admitância Y C corresponde a impedância Z C .

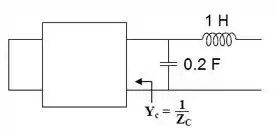
Passo 3

A impedância Z C corresponde a admitância Y C :

Z C = 1 Y C = 5 s 2 + 8 3,4 s

Para determinar os valores de L 3 e C 4 nós devemos simplificar a fração através da divisão de polinômios:

Z C = 5 s 2 + 8 3,4 s = 1,47 s + 8 3,4 s = 1,47 s + 1 0,425 s = s L 3 + 1 s C 4

L 3 = 1,47   H ,     C 4 = 0,425   F

Assim, o circuito cascata é igual a:

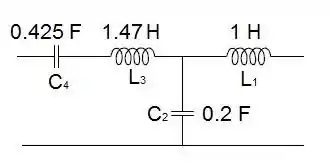
Resposta

Ver Outros Exercícios desse livro