Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 6
As bobinas na Figura 13.75 têm e coeficiente de acoplamento . Determine e dado que e ), .
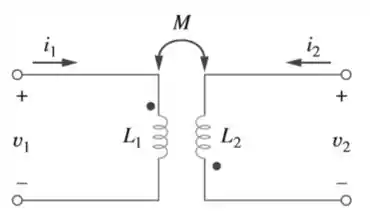
Passo 1
Seguinte pessoal, vamos analisar os dados que a questão nos dá e a partir daí jogar nas fórmulas... sem erro!
De cara podemos calcular a induntância mútua:
Para cada indutor, transformemos em :
Passo 2
Analisaremos o circuito que ficou:
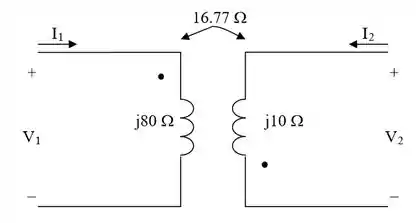
Disso, temos que:
Mas, Substituindo isso na equação de , temos:
Fazendo a mesma coisa na equação de , substituindo as duas correntes, temos que:
Resposta
Exercícios de Livros Relacionados
a) Mostre que as equações diferenciais deduzidas em (a) do Exemplo 6.6 podem ser rearranjadasda seguinte forma:b) Mostre que as soluções para i1 e i2 dadas em (b) do Exemplo 6.6 satisfazem as equações
a) Mostre que os dois enrolamentos acoplados da Figura P6.40 podem ser substituídos por um único enrolamento com uma indutância de Lab = L1+ L2 + 2M. (Sugestão: expresse vab em função de iab.)b) Mostr
A montagem física de quatro pares de enrolamentos acoplados magneticamente é mostradana Figura P6.43. Suponha que o fluxo magnético esteja confinado ao material do núcleo em cada estrutura. Mostre dua
Dois enrolamentos magneticamente acoplados têm autoindutâncias de 60 mH e 9,6 mH, respectivamente. A indutância mútua entre eles é 22,8 mH.a) Qual é o coeficiente de acoplamento?b) Qual é o maior valo