Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 6.Problemas - Ex. 43

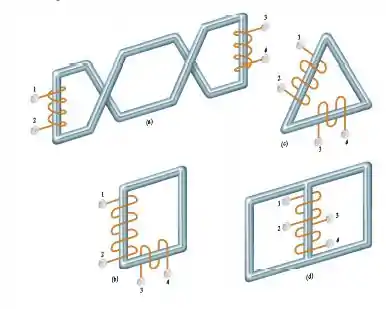
A montagem física de quatro pares de enrolamentos acoplados magneticamente é mostrada

na Figura P6.43. Suponha que o fluxo magnético esteja confinado ao material do núcleo em cada estrutura. Mostre duas possíveis localizações para a marcação de pontos em cada par de enrolamentos.

Passo 1

Falaaa, pessoal! Como vocês estão? Então vamo lá. [a] Ponto terminal 1; o fluxo é para cima na bobina 1-2 e para baixo na bobina 3-4. Atribua a corrente ao terminal 4; o fluxo está para baixo na bobina 3-4. Portanto, dot terminal 4. Portanto, 1 e 4 ou 2 e 3.

[b] Ponto terminal 2; o fluxo é ascendente na bobina 1-2 e da direita para a esquerda na bobina 3-4. Atribua a corrente ao terminal 4; o fluxo é da direita para a esquerda na bobina 3-4. Portanto, dot terminal 4. Portanto, 2 e 4 ou 1 e 3.

[c] Ponto terminal 2; o fluxo é ascendente na bobina 1-2 e da direita para a esquerda na bobina 3-4.

Atribua a corrente ao terminal 4; o fluxo é da direita para a esquerda na bobina 3-4. Portanto, dot terminal 4. Portanto, 2 e 4 ou 1 e 3.

[d] Ponto terminal 1; o fluxo é para baixo na bobina 1-2 e para baixo na bobina 3-4. Atribua a corrente ao terminal 4; o fluxo está para baixo na bobina 3-4. Portanto, dot terminal 4. Portanto, 1 e 4 ou 2 e 3.

Resposta

Resposta nos passos

Exercícios de Livros Relacionados

Duas bobinas ligadas de forma a favorecer a conexão em série possuem indutância total de 500m H . Quando ligadas em uma configuração de forma a se opor à conexão em série, as bobinas apresentam uma in

Duas bobinas estão acopladas mutuamente, com L 1=50m H , L 2=120m Hek=0,5 . Calcule a máxima indutância possível se:As duas bobinas estiverem conectadas em sérieAs duas bobibnas estiverem conectadas e

Para as bobinas acopladas na Figura 13.74a, demonstre que L e q = L 1 + L 2 + 2 M Para as bobinas acopladas na Figura 13.74b demonstre que L e q = L 1 L 2 - M 2 L 1 + L 2 - 2 M

As bobinas na Figura 13.75 têm L 1 = 40m H , L 2 = 5m H e coeficiente de acoplamento k =0 , 6 . Determine i 1 ( t ) e v 2 ( t ) dado que v 1 ( t ) = 20c o sv t e i 2 ( t ) = 4s e nv t , v=2.000r a d /

Considere o circuito da Figura 13.76 e determine V o .