Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.8 - Ex. 3

CaIcule i no Ex. 8.8.1, se i_g = 10 [u (t) - u (t - 1)] A

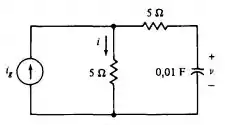
Passo 1

Fala aí pessoal tudo blz?

Nessa questão ele deseja calcular o i , dado

i_g = 10 [u (t) - u (t - 1)] A

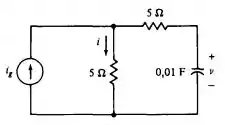
Só vem, confia

Passo 2

Sabendo que,

i_g = 10 [u (t) - u (t - 1)] A , temos para este circuito RC

i = i_n + i_f

i = (u ( t ))/(10.0,01) T u (t) = i = 1

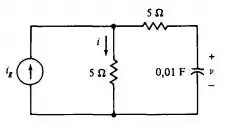
Ficando,

i = 10 (1 - 0,5 e^(- 10 t)) . u (t) A - (1 - 0,5 e^(- 10 ( - 1 ) t)) . u (t - 1) A

Bem rapidinha né rsrs. Espero ter colaborado para o seu desempenho, bons estudos e até a próxima.

Resposta

i = 10 (1 - 0,5 e^(- 10 t)) . u (t) A - (1 - 0,5 e^(- 10 ( - 1 ) t)) . u (t - 1) A

Exercícios de Livros Relacionados

Calcule vs ev g = 5 e - t u t V e não existe energia inicial armazenada. (Este circuita é como o integrador da figura 8.24, exceto que o capacitor tem um resistor em paralelo com ele, tornando-o um ca
Calcule as respostas ao degrau iev [ i g = u t A ] .
Reduza (8.22) a forma de (8.23)v (t) = 12 (1 - e^(- t)) [u (t) - u (t - 1)] + 12 (1 - e^(- t)) e^(- (t - 1)) u ( t - 1 ) Em,v (t) = 12 (1 - e^(- t)) u (t) - 12 ( 1 - e^(- (t - 1)) ) u ( t - 1 )
Use a super posição para calcular v na Fig. 8.29 se: R 1 = 2 Ω ,R 2 = 3 Ω ,C = 0,1F ,V 0 = 8V ,V 1 = 12VeI 1 = 2A