Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 30

8.30) Calcule v1 para t > 0, se não existe energia inicial armazenada.

Passo 1

E aí galerinhaaa!! Vamos resolver essa questão juntinhos, beleza??

Nosso circuito é mostrado abaixo:

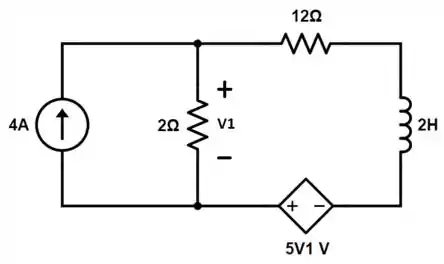
Primeiro, podemos verificar que se trata de um circuito RL excitado, porque apresenta uma fonte de corrente independente. Para o caso de circuito excitado, a resposta v1(t) será dada da seguinte forma:

v 1 t = v 1 n + v 1 f       ( 1 )

Em que v 1 n é a resposta natural do sistema e v 1 f é a resposta forçada.

Passo 2

Agora, vamos achar ambas as respostas do nosso circuito.

Para a resposta natural, devemos nos lembrar que esta é obtida somente pela dissipação da energia armazenada no indutor. Logo, para calculá-la temos que retirar toda fonte independente do circuito como abaixo:

Fazendo a famosa LKT obtemos:

2 d i d t - 5 v 1 n + 2 i + 12 i = 0       ( 2 )

Porém,

v 1 n = - 2 i       ( 3 )

Substituindo (3) em (2) temos:

2 d i d t + 10 i + 2 i + 12 i = 0 ⇒

2 d i d t + 2 4 i = 0 ⇒

d i d t + 12 i = 0       ( 4 )

Substituindo d i d t por λ em (4):

λ + 1 2 = 0 ⇒

λ = - 1 2

Logo, temos:

i t = A e λ t = A e - 1 2 t   A

Chegamos então que v 1 n é:

v 1 n = - 2 i = - 2 A e - 1 2 t = B e - 1 2 t   V       ( 5 )

Passo 3

Calma que falta pouco galerinhaaa!

Vamos terminar achando agora a resposta forçada do nosso circuito. Temos que lembrar que pro cálculo dessa resposta devemos considerar o sistema em regime permanente CC, ou seja, o indutor se comportará como um curto-circuito, lembram disso??

Bora transformar também a fonte de corrente numa fonte de tensão pra facilitar nossa vida?? Vejam só como fica nosso circuito:

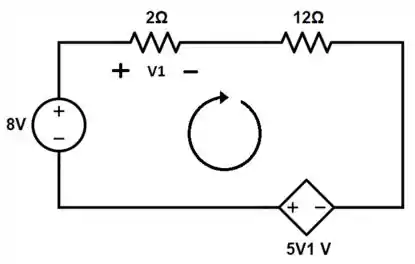
Fazendo novamente a nossa bela LKT:

- 5 v 1 f - 8 + 2 i + 12 i = 0       ( 6 )

Porém,

v 1 f = 2 i       ( 7 )

Substituindo (6) em (7) temos:

- 10 i + 2 i + 12 i = 8 ⇒

4 i = 8 ⇒

i = 2 A

Logo, v 1 f é:

v 1 f = 2 i = 4 V

Passo 4

Por fim, substituindo os valores encontrados na equação (1):

v 1 t = B e - 1 2 t + 4

Só falta achar o coeficiente B através da condição inicial e enfim matamos essa questão!!

Foi dado no enunciado que a energia inicial armazenada é nula. Então, i L 0 + = i L 0 - = 0 , então v 1 0 + = v 1 0 - = 8 .

v 1 0 = B e - 1 2 * 0 + 4 = 8 ⇒

B = 4

Concluindo, chegamos na equação final de v1(t):

v 1 t = 4 e - 1 2 t + 4   V

Prontinhooo, finalizamos essa! Bora pra mais uma??

Resposta

v 1 t = 4 1 + e - 1 2 t   V

Exercícios de Livros Relacionados

A questão pede a porcentagem de energia armazenada que será dissipada no resistor de 6Ω . Então simbora calcular isso!
A questão descreve um circuito que está a bastante tempo em um estado, o que ela quer que você saiba, é a mudança de comportamento do circuito a partir da abertura da chave. Portanto, let’s go e vamos
A questão descreve um circuito RL, que em um dado período muito longo, em t = 0, a chave é fechada e a partir disso, analisaremos o circuito. Então chega junto e vamos resolver!
A chave no circuito da Figura P7.4 esteve na posição 1 por um longo tempo. Em t = 0 , ela passa instantaneamente para a posição 2. Determine v o t para t ≥ 0 + .
A chave no circuito da Figura P7.10 esteve na posição 1 por um longo tempo. Em t = 0 , ela passa instantaneamente para a posição 2 . Determine o valor de R de modo que 10 % da energia inicial armazena