Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 13
Se . Calcule (a) , (b) , (c) e (d) em e em .
Passo 1
Iae, meus queridos! Td blzinha?
Essa questão nos pede bastante coisas, então partiu!
Primeiro de tudo, vamos verificar se o capacitor está totalmente carregado no instante . Podemos verificar quando o exercício diz que , ou seja, . Além disso se a corrente é , podemos afirmar que também é pela equação.
Já temos os primeiros resultados!
Também podemos encontrar facilmente. Se , a tensão no resistor abaixo do capacitor é também e como o capacitor está totalmente carregado a tensão nele será a tensão no resistor paralelo a ele.
A questão já nos deu a corrente , . Vamos calcular a tensão no resistor de apicando a Lei de Ohm.
Observando o circuito, vemos que o resistor de está em paralelo com o resistor de . Percebeu a mágica? Vamos aplicar a Lei de Ohm nele e encontrar .
Viu como tudo corre naturalmente? 😎
Passo 2
Para calcular , temos que calcular a resistência equivalente do circuito com a chave aberta, vista pelo capacitor. Seguindo as seguintes etapas...
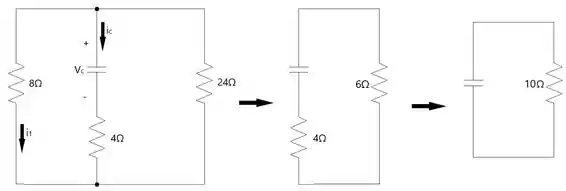
Vemos que a resistência equivalente é .
No instante em que a chave é aberta, o capacitor está completamente carregado, isso nos diz que , sendo assim, a tenção na resistência equivalente é a tensão é , com isso em mente, podemos aplicar a Lei de Ohm e encontrar .
Tranquilo?
Agora vamos calcular a tensão no resistor de , a qual será a mesma no resistor do equivalente paralelo entre e , no caso, o resistor de do segundo circuito da imagem acima.
Aplicando a Lei de Ohm no resistor , encontraremos .
Por fim, precisamos calcular .
Iae, achou fácil?
Resposta
(a) , .
(b) , .
(c) , .
(d) , .