Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 3.Problemas - Ex. 24
Calcule i.
Passo 1
Dado o circuito:
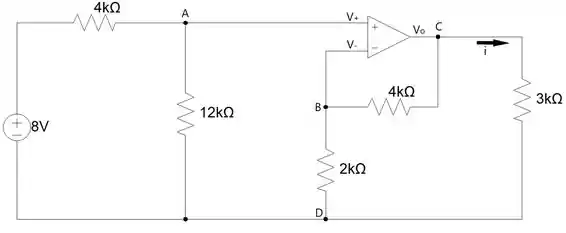
Vamos calcular a tensão no ponto A, a qual vai ser a mesma tensão no ponto B, já que . Como , toda a corrente que flui para o nó A, passa pelo resistor de 12kΩ, portanto podemos analisar como se fosse um circuito de apenas uma malha.
Aplicando a Lei de Ohm:
Calculando a tensão em A:
Passo 2
A corrente que passar pelo nó B, é a mesma que passa pelo nó C, como temos a tensão em B, podemos calcular essa corrente aplicando a Lei de Ohm.
Com esse valor em mãos, podemos calcular aplicando a Lei de Ohm com a resistência equivalente entre os nós C-D: → .
Passo 3
Por fim, já que temos a tensão e a resistência, calculamos a corrente i pela Lei de Ohm.
Resposta
Exercícios de Livros Relacionados
No amplificador diferencial mostrado na Figura P5.34, qual é a faixa de valores de R x que resulta em um FRMC ≥ 1.500?
Projete um amplificador diferencial (Figura 5.15) que obedeça ao seguinte critério: v o=3 v b-4 v a . A resistência vista pela fonte de sinal v bé470k V é , e a resistência vista pela fonte de sinal v
O amp op no circuito da Figura P5.32 é ideal. a) Desenhe um gráfico de v ov e r s u saq u a n d oR f=4 R 1ev g=2V . Use incrementos de 0,1 e observe, por hipótese, que 0 ≤a≤ 1,0 . b) Escreva uma equaç
a) Use o princípio da superposição para deduzir a Equação 5.22. b) Deduza as equações 5.23 e 5.24.
Suponha que o amp op ideal no circuito apresentado na Figura P5.38 esteja operando em sua região linear. a) Mostre que v o=R 1+R 2 R 1 v s . b) O que acontece se R 1 → ∞eR 2 →0 ? c) Explique por que e