Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 16.1 - Ex. 4

Calcule as correntes fasoriais I_1 e I_2 .

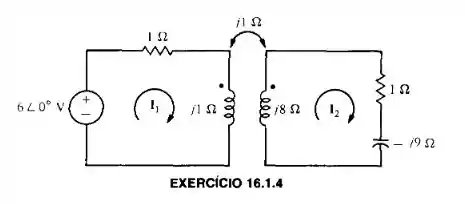
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Essa questão é bem simples e se resume a uma LKT, a primeira malha é dada por

- 6 /_ 0 ° + 1 I_1 + j I_1 + j I_2 = 0

Rearranjando os termos, nós temos que

I_1 (1 + j) + j I_2 = 6 /_ 0 °

Já na segunda malha, nós temos que

j 8 I_2 + I_2 - j 9 I_2 - j I_1 = 0

Desenvolvendo o termo, nós temos que

- j I_1 + I_2 (1 - j) = 0

Passo 2

Temos duas malhas, então, vamos resolver matrizes, logo, nós temos que

(|[[6,/_,0,°,j],[0,(,1,-,j,)]]|)/(|[[(,1,+,j,),j],[+,j,(,1,-,j,)]]|) = (6 ( 1 - j ))/((1 - j) (1 + j) - ( + j^2 ))

No final, nós temos que

(6 (1 - j))/(3) = (6 - 6 j)/(3) = 2 - 2 j

Passo 3

Para encontrar a segunda corrente fasorial, nós temos que

(|[[(,1,+,j,),6,/_,0,°],[j,0]]|)/(|[[(,1,+,j,),j],[+,j,(,1,-,j,)]]|) = (6 j)/(3) = 2 j

Logo, I_1 e I_2 são iguais a

I_1 = 2 - 2 j

I_2 = 2 j

Resposta

I_1 = 2 - 2 j

I_2 = 2 j

Exercícios de Livros Relacionados

Calcule M , se L_1 = 0,2 H , L_2 = 0,8 H e (a) k = 1 , (b) k = 0,5 e (c) k = 0,02 .
Determine a energia armazenada em t = 0 , para todos os casos do Ex. 16.1.2.
No circuito da figura 16.3 a .L 1 = 4 H ,L 2 = 6 HeM = 3 H . Calcule v 1ev 2 , no momento em que as taxas de variação das correntes são, d i 1 d t = - 2 A s , d i 2 d t = 2 A s
Calcule V , na Figura 16.18(a), usando o circuito equivalente da Figura 16.21(c).