Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.3 - Ex. 1

Mostre que a frequência de ressonância. no caso da função do Ex. 15.2.1, coincide com a frequência para a qual a função e real.

Passo 1

Iae, meus queridos! Td certinho??

Se essa questão está difícil, não se preocupe que após essa resolução, ela vai parecer fácil! 😎

Vamos escrever a Função H s e fazer a substituição de s → j ω

H s = 2 s s 2 + 0,2 s + 1 → H j ω = j 2 ω - ω 2 + j 0,2 ω + 1

Vamos manipular H j ω para tirar o termo imaginário do denominador.

H j ω = j 2 ω ( 1 - ω 2 ) + j 0,2 ω

H j ω = j 2 ω ( 1 - ω 2 ) + j 0,2 ω · 1 - ω 2 - j 0,2 ω 1 - ω 2 - j 0,2 ω

H j ω = 0,4 ω 2 + j 2 ω - 2 ω 2 ω 4 - 1,96 ω 2 + 1

Passo 2

Vamos ignorar a parte imaginaria da equação, assim, R e   H j ω será.

R e   H j ω = 0,4 ω 2 ω 4 - 1,96 ω 2 + 1

Com o auxílio de uma calculadora, uma calculadora gráfica ou algum método de cálculo de máximos de funções, podemos encontrar o valor para ω ≥ 0 , em que a função seja máxima.

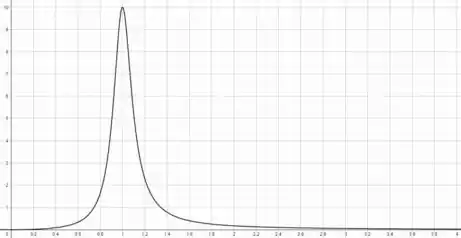
A partir do gráfico acima, vemos que quando ω = 1 , a função atinge seu valor máximo.

Iae, foi tranquilo?

Resposta

ω = 1

Exercícios de Livros Relacionados

Calcule os parâmetros y da rede indicados. Coloque um resistor de 1 - Ω nos terminais de saída e calcule a funçăo de rede resultante V / - V 1
Calcule H ( s ) se a resposta é v . Use o resultado para calcular a resposta forçada, se v g = 5 cos ⁡ tV .
Calcule H ( s ) se a resposta é (a) I_1 ( s ) , (b) I_0 ( s ) e (c) V_0 ( s ) .
Calcule a condutância e a susceptância, se Z é (a) 3 + j 4 , (b) 0,4 + j 0,3 e (c) 2 2 ∠ 45 °
Calcule a impedância vista pelos terminais da fonte na Figura 10.4, nas formas retangular e polar.