Calcule a potência entregue a R quando (a) , (b) e (c) quando recebe a potência máxima.

Passo 1
E aí, galerinha! Tudo tranks? Simbora pra mais uma questãozinha aí!?
Bom! Precisamos encontrar o circuito equivalente de Thévenin para o circuito como no esquema abaixo...
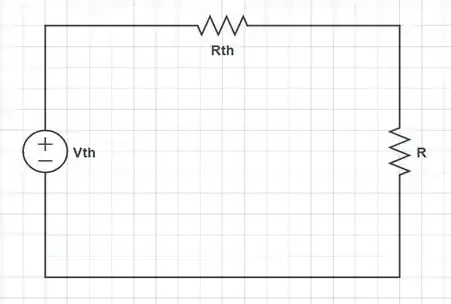
Passo 2
Para encontrar a resistência de Thévenin, vamos começar excluindo todas as fontes independentes desse circuito...
Com isso, ficamos com aquelas duas resistências de e em série com a de ... Sendo assim;
Passo 3
Para achar então, vamos recorrer ao método da superposição...
Vamos começar excluindo a fonte de corrente de , que vai virar um circuito aberto e deixar apenas a fonte de tensão de ...
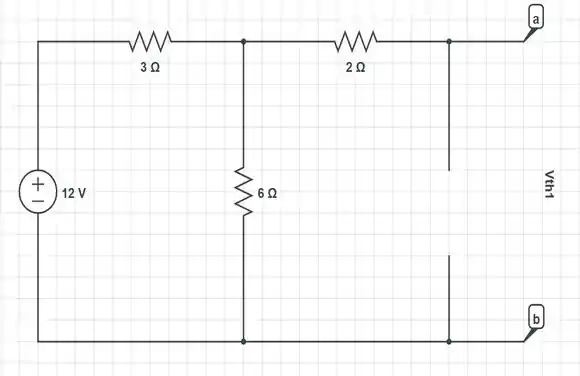
Então, pra achar esse primeiro basta usar o método do divisor de tensão...
Em seguida, vamos deixar apenas a fonte de corrente, curto-circuitando a fonte de tensão de ... Isso nos leva à...
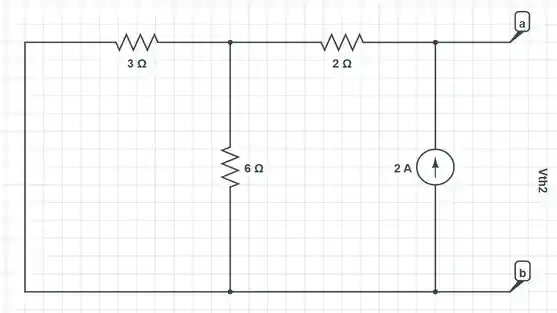
Com isso, como podemos ver acima, será dada por...
Aí, pra achar final basta somar as duas fontes...
Passo 4
A forma final do nosso circuito fica então, assim...
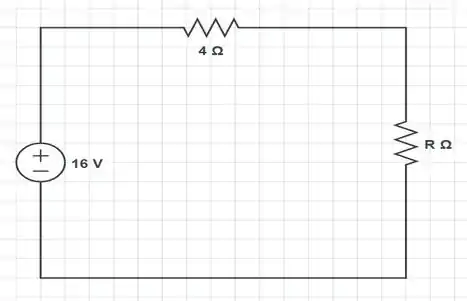
Onde pelo que podemos ver, a potência entregue a será dada pela seguinte fórmula...
a) E então, substituindo :
b) E depois, :
c) A potência máxima, por sua vez, ocorre quando e vale...
A potência máxima sempre acontece quando ! É por isso que ela se dá em .
Sucesso? Até a próxima, guys!
Resposta
a)
b)
c)