Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 14
Calcule para , se o circuito está em regime permanente em .
Passo 1
Iae, meus queridos! Td certinho?
A questão nos disse que o circuito está em circuito permanente no instante , vamos ver como visualizamos o circuito nesse instante.
Analisando o circuito nessa configuração, vemos que possui apenas uma malha, dessa forma, podemos calcular a corrente dessa malha para encontrar a tensão inicial de e aplicando a Lei de Ohm.
Portanto:
Passo 2
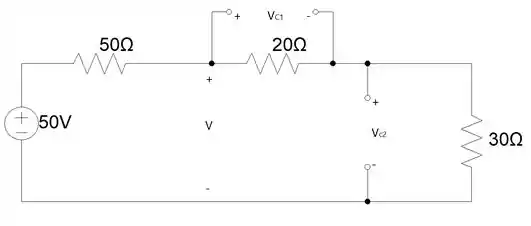
Para , o circuito fica assim:
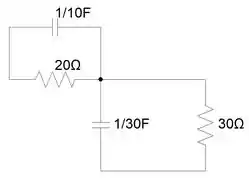
Mas, caso você não esteja entendendo direito como esse circuito vai se comportar dessa forma, podemos visualiza-los como dois circuitos distintos:
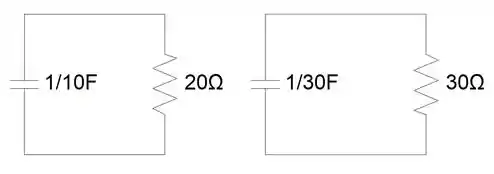
Agora temos mais intimidades.
Vamos montar a equação de tensão do primeiro circuito:
Agora, o mesmo para o segundo circuito:
Por fim, somamos as duas tensões para encontrarmos o valor de .
Iae, gostou da questão? Toma uma água e bora pra outra!