Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.6 - Ex. 2
Calcule a indutância equivalente. (Os valores dos indutores são dados em mH.)
Passo 1
Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 5 minutos?? Bora. Bom, nosso enunciado nos pede para achar a indutância equivalente. Puts!! Parece difícil?? Vai ser tranquilo. Partiu??
Passo 2
Ok, agora o nosso problema vai ser relembrar qual a fórmula de um indutor em série e em paralelo. Responde Aí!! Lembrou?? Não?!
Vamos usar a associação em paralelo como:
E para a associação em série.
Passo 3
Agora vamos analisar esse circuito.
Começando pelo lado direito, temos dois indutores em paralelo.
Assim, pela fórmula, resultará em:
O circuito resultante será:
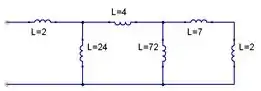
Agora, novamente no lado direito, temos dois indutores em série. Pela fórmula
O circuito resultante será:
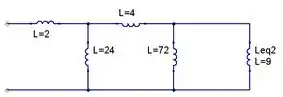
Novamente no lado direito, temos dois indutores em paralelo. Pela fórmula:
O circuito será:
Está cansado?? Aguenta aí que estamos quase acabando!!
Novamente no lado direito, temos dois indutores em série. Pela fórmula:
O circuito resultante será:
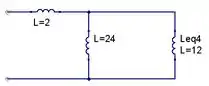
Agora, novamente no lado direito, temos dois indutores em série. Pela fórmula:
O circuito será:
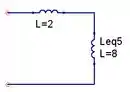
Para finalizar, temos dois indutores em série. Pela fórmula:
Tranquilo essa hein!!