Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 5.Problemas - Ex. 38

Calcule a potência máxima que pode ser entregue a R se (a) R 1 = 12 Ω e (b) R 2 = 30 Ω .

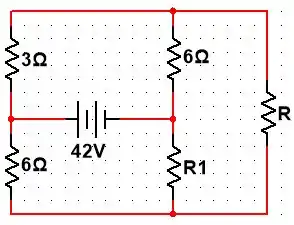
Passo 1

Eaeee meu gafanhoto!! Bora pra mais uma sobre máxima transferência de potência?!

Para isso a gente sabe que:

P m á x = V T H 2 4 R T H

Em que:

  • P m á x é a potência máxima;
  • V T H é a tensão de Thévenin;
  • R T H é a resistência de Thévenin.

Obs: A maior transferência de potência para uma carga R será quando R = R T H .

Passo 2

Para descobrirmos a resistência de Thévenin R T H temos basicamente que trocar a fonte de tensão por um curto circuito. Logo, temos para R 1 = 12 Ω :

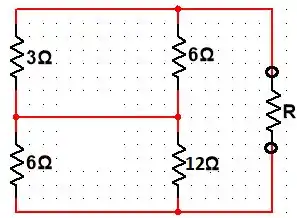
Analisando a figura acima podemos dizer que:

R T H = ( 3 | | 6 ) + ( 6 | 12 ∴

R T H = 2 + 4 = 6 Ω

Logo, R = R T H = 6 Ω .

Passo 3

Para descobrirmos V T H , temos que V T H = V ' :

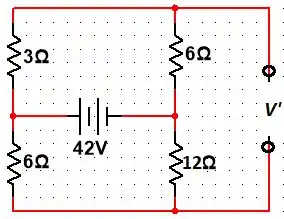
Aplicando divisor de tensão para descobrir a tensão no resistor de 6 Ω de cima:

V 6 Ω = 42 × 6 6 + 3 = 28   V

Aplicando divisor de tensão no resistor de 12 Ω :

V 12 Ω = 42 × 12 12 + 6 = 28 V

Assim, temos que:

V T H = V ' = V 6 Ω + V 12 Ω ∴

V T H = 28 + 28 = 56   V

Passo 4

Assim, a potência máxima do circuito para R = 12 Ω é dada por:

P m á x 12 Ω = 56 2 4 × 6 ∴

P m á x 12 Ω = 130.67 W

Passo 5

Agora, fazendo a meeesma coisa para R = 30 Ω , temos:

R T H = ( 3 | | 6 ) + ( 6 | 30 ∴

R T H = 2 + 5 = 7 Ω

Para a tensão de Thévenin, temos:

V T H = V 6 Ω + V 30 Ω ∴

V T H = 28 + 42 × 30 30 + 6 ∴

V T H = 63 V

Assim, a potência máxima do circuito para R = 30 Ω é dada por:

P m á x 30 Ω = 63 2 4 × 7 ∴

P m á x 30 Ω = 141,75 W

Tranquilo ne?? Vamos para outra!!

Resposta

P m á x 12 Ω = 130.67 W

P m á x 30 Ω = 141,75 W

Exercícios de Livros Relacionados

Repita o Pron. 1.24 (a) para i = 2 ( e - 2 t - 1 ) A ,t0 = 0 ,t0
Considera que a corrente que entra pelo terminal positivo de um elemento seja i = 2 s e n 6 tA ,t0 = 0 ,t0 (a)Se a tensão é v = 4 d i d t V mostre que a energia entregue ao elemento é não-negativa par
Calcule a potência máxima que pode ser entregue ao resistor de R no circuito do Prob. 5.12.
A corrente que entra pelo terminal positivo de um elemento e i=- 4 e - 2 tA . Calcule a potência entregue ao elemento em função do tempo e a energia entregue ao elemento para t0 , se a tensão e (a) v=
Se a corrente que entra pelo terminal positivo de um elemento e i=- 4 e - 2 tA e a tensão e v=8 iV , calcule a energia entregue ao elemento entre 0 e 1s .