Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 10
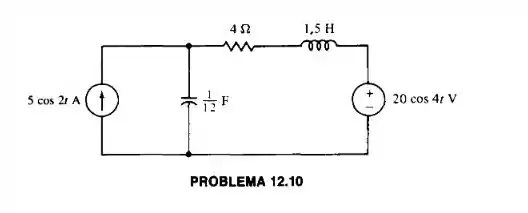
Calcule a potência média entregue ao resistor de .
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Vamos lá, existem duas fontes com frequências diferentes , nesse caso, nós teremos que usar superposição, calcular a potência que cada fonte manda para o resistor e depois, por fim, somar. Tendo isso em mente, vamos analisar primeiro o circuito com a fonte de corrente, com isso, nós temos a seguinte configuração
Para saber a corrente a que passa pelo resistor, vamos usar a Lei de Ohm, com isso
Convertendo para fasores
Já para o caso da tensão, nós obtemos
E com isso, já podemos verificar a potência no resistor
Substituindo os valores e lembrando que o cosseno é unitário para o resistor, nós obtemos o seguinte resultado
Passo 2
E vamos para a fonte de tensão, então, por superposição, nós temos a seguinte configuração de circuito
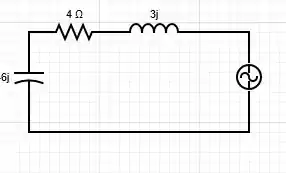
O raciocínio, corrente, tensão e potência. Percebeu que todos os componentes estão em série? Logo, vamos usar basicamente de novo a Lei de Ohm, pegando a impedância equivalente
Fazendo a conversão para fasores, nós temos que
E a tensão no resistor,
Com isso, a potência é igual a
Passo 3
Ok, temos as duas potências, logo, neste momento, necessitamos apenas fazer a diferença das duas potências encontradas, com isso, nós temos que
Substituindo os valores, nós temos que