Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 22
Calcule a tensão em regime permanente, se
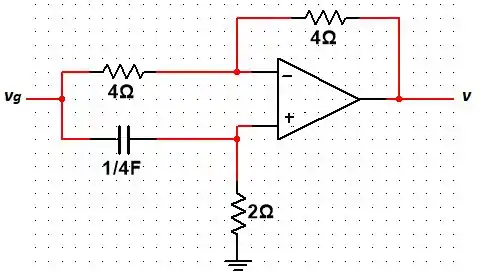
Passo 1
Opaa mais um Amp Op!! Boraa!!
Bora continuar com aquele padrãozinho... Primeiro vamos analisar o circuito com o capacitor em forma de reatância.
Lembrando que:
Em que .
Logo, temos:
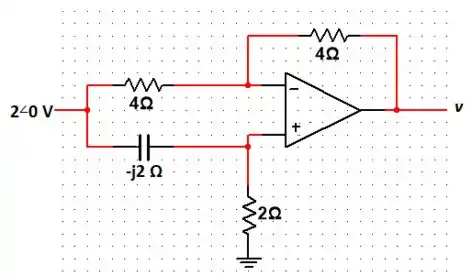
Passo 2
Sabemos que a tensão na entrada inversora é a mesma na entrada não inversora ne (considerando um amp op ideal viu?!). Assim, fazendo o divisor de tensão, podemos descobrir a tensão nas entradas. Veja nesse ramo:
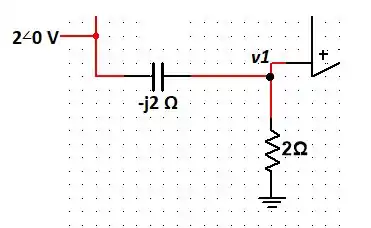
Pelo divisor de tensão, temos:
Passo 3
Agora, analisando a parte de cima do circuito e atribuindo a direção da corrente, temos que:
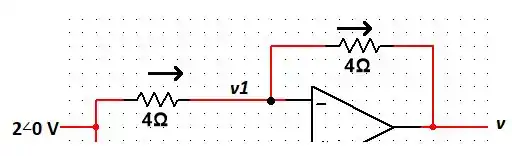
Assim, substituindo :
Fácil fácil né??? Bora pra próxima haha!
Resposta
Exercícios de Livros Relacionados
O PSpice é capaz de tratar um circuito com duas fontes independentes de frequências diferente. Verdadeirob) falso
Consulte o circuito da Figura 10.49. A impedância equivalente de Norton nos terminais a-b é: - j 4Ω b) - j 2Ω c) j 2Ω d) j 4Ω
Consulte o circuito da Figura 10.49. A impedância equivalente de Norton nos terminais a-b é: - j 4Ω b) - j 2Ω c) j 2Ω d) j 4Ω
Consulte o circuito da Figura 10.47 e observe que as duas fontes não têm a mesma frequência. A corrente i x t pode ser obtida por:Transformação de fontesTeorema da superposiçãoPSpice
No circuito da Figura 10.48, a tensão de Thévenin nos terminais a-b é: 3.535 ∠ - 45 °V b) 3.535 ∠ 45 °V c) 7.071 ∠ - 45 °V d) 7.071 ∠ 45 °V