Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 28
Calcule a corrente em regime permanente, se .
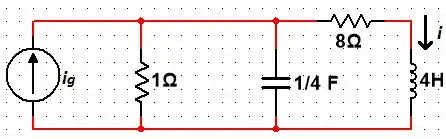
Passo 1
E esse valor de aí ein? Como é que é????
E eu digo: caaaaaalma!! Basta a gente interpretar cada termo separadamente de . É a famosa superposição novamente dando um xeirinho no nosso cangote haha!
Passo 2
Vamos para o primeiro caso, em que .
Note que, por se tratar de uma fonte de corrente contínua, vale lembrar que:
- Capacitores são vistos como circuitos abertos;
- Indutores são vistos como curto circuitos.
Logo, temos a seguinte representação:
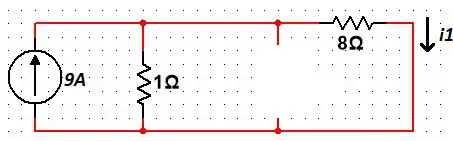
Pelo divisor de corrente, temos que:
Passo 3
Agora, vamos para o segundo caso, em que .
Passando os valores da fonte para a forma polar e enxergando o capacitor e o indutor em forma de reatâncias.
Lembrando que:
Em que . Temos:
Fazendo a impedância equivalente entre o resistor de e a reatância de e, logo em seguida fazendo o divisor de corrente. Temos que:
Assim:
Passo 4
Agora, vamos para o terceiro caso, em que .
Passando os valores da fonte para a forma polar e enxergando o capacitor e o indutor em forma de reatâncias.
Em que . Temos:
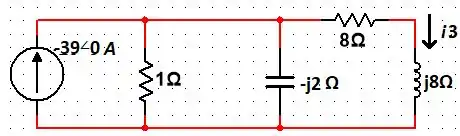
Fazendo a impedância equivalente entre o resistor de e a reatância de e, logo em seguida fazendo o divisor de corrente. Temos que:
Assim:
Passo 5
Agora, vamos para o quarto caso (aleluuiaaa), em que .
Passando os valores da fonte para a forma polar e enxergando o capacitor e o indutor em forma de reatâncias.
Em que . Temos:
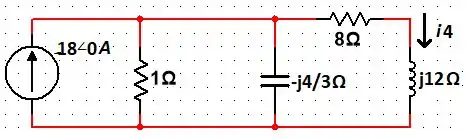
Fazendo a impedância equivalente entre o resistor de e a reatância de e, logo em seguida fazendo o divisor de corrente. Temos que:
Assim:
Passo 6
Prontinho, agora sabemos que:
Substituindo os valores que encontramos, temos que: