Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 23

Calcule a resposta forçada v , se v_g = 2 cos t V .

Passo 1

Eitaaa que essa aí é maiorzinha ein?? Mas se acalme que vai dar certo haha!

Bora continuar com aquele padrãozinho... Primeiro vamos analisar o circuito com o capacitor em forma de reatância.

Lembrando que:

X_C = - (j)/(omega C)

Em que omega = 1 r a d // s .

Logo, temos:

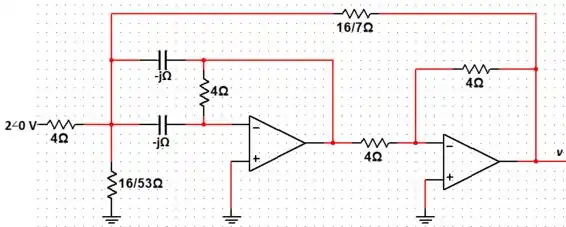
Passo 2

O circuito é grandinho mas tem uma coisa que facilita muuuuuito!! Se vc olhar nas entradas não inversoras dos dois Amps Ops estão ligadas ao terra, ou seja, a tensão em cada uma equivale a 0V. Não entendeu no que isso vai te facilitar? Então vem comigo haha!

Vamos selecionar os nós e atribuir direções da corrente aqui para podermos analisar melhor a situação:

Obs: coloquei o 0 V ali só pra destacar o que tinha falado antes viu? ;)

Passo 3

Perceba esse seguinte ramo:

A partir dele, podemos afirmar que:

(v 2 - 0)/(- j) = (0 - (- v))/(4) :.

v 2 = - (j v)/(4)

Passo 4

Agora, aplicando a Lei de Kirchhoff das Correntes no nó v 2 para o nosso circuito completo, temos:

(2 - v 2)/(4) = (v 2)/((16)/(53)) + (v 2)/(- j) + (v 2 - (- v))/(- j) + (v 2 - v)/((16)/(7))

Substituindo v 2 que encontramos anteriormente, temos:

(2 - ( - (j v)/(4) ))/(4) = (( - (j v)/(4) ))/((16)/(53)) + (( - (j v)/(4) ))/(- j) + (( - (j v)/(4) ) - (- v))/(- j) + (( - (j v)/(4) ) - v)/((16)/(7)) :.

((1)/(2) + (j v)/(16)) = (- (j 53 v)/(64)) + ((v)/(4)) + ((v)/(4) + j v) + (- (j 7 v)/(64) - (7 v)/(16)) :.

Multiplicando tudo por 16 a fim de simplificar, temos:

8 + j v = - (j 53 v)/(4) + 8 v + j 16 v - (j 7 v)/(4) - 7 v :.

v = 8 /_ 0 ° V

Prontinho!! É só ter cuidado para não se confundir, o resto é simples!! ;)

Resposta

v = 8 cos (t) V

Exercícios de Livros Relacionados

O amp op no circuito visto na Figura P9.72 é ideal. Determine a expressão de regime permanente para vo(t) quando vg = 2 cos 106t V.
O valor de k no circuito da Figura P9.74 é ajustado de modo que Zab seja puramente resistiva quando v = 4 krad/s. Determine Zab.
Três ramos com impedâncias de 3 + j4 V, 16 - j12 V e -j4 V, respectivamente, estão ligados em paralelo. Quais são (a) a admitância, (b) a condutância e (c) a susceptância (em milissiemens) equivalente
Um resistor de 25 V, um indutor de 50 mH e um capacitor de 32 mF estão ligados em série. Os elementos ligados em série são energizados por uma fonte de tensão senoidal cuja tensão é 25 cos (500t - 60°