Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 38

8.38) Calcule v para todo t, se (a) vg = 12u(t) V e (b) vg = 12[u(t)-u(t-1)]V.

Passo 1

E aí galerinhaaa!! Vamos resolver essa questão juntinhos, beleza??

Nosso circuito é mostrado abaixo:

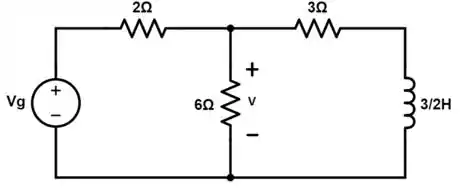
Primeiro, temos a letra (a), em que . Nesse caso, devemos analisar o circuito em dois momentos: t 0.

Para t

Como é nulo e não consideramos nenhuma condição inicial para a energia armazenada no indutor assume-se que esta é nula também. Portanto,

Para t > 0 temos:

Resposta ao degrau é dada na forma:

Onde,

é a resistência equivalente vista pelo indutor. Para achá-la, lembra que devemos curto-circuitar fonte de tensão e abrir fonte de corrente?? Sendo assim, temos:

Substituindo (3) em (2):

E por divisão de tensão e pela Lei de Ohm, a resposta forçada é o valor em regime permanente. Lembrando que indutor se comporta como um curto-circuito em regime permanente temos:

Logo, associando as equações (4) e (5):

Sabemos que , portanto:

Chegamos que:

Passo 2

Agora, para a letra (b), em que , a diferença é que a resposta é composta de três componentes: t 1.

Para os dois primeiros casos a resposta é a mesma da letra (a), ou seja:

Falta acharmos então a resposta do circuito sem fontes para t > 1. Para esse último caso, a equação de v é dada na forma:

Para t = 1- (instante imediatamente anterior a t = 1), a solução da resposta ao degrau nos dá:

Visto que a corrente no indutor é contínua, , onde 1+ é o instante imediatamente após t = 1. Portanto,

Nossa solução será:

A solução completa para a letra (b) fica então:

Prontinhooo, essa teve muito cálculo, mas deu pra pegar a ideia, né? Bora pra mais uma??

Resposta

Exercícios de Livros Relacionados

As duas chaves no circuito visto na Figura P7.6 são sincronizadas. Elas estiveram fechadas por um longo tempo antes de se abrirem em t = 0 .a) Em quantos microssegundos, depois da abertura das chaves,

No circuito da Figura P7.7, a chave esteve fechada por um longo tempo antes de ser aberta em t = 0 .a) Determine o valor de L de modo que v 0 t seja igual a 0,5 v 0 0 + quando t = 1m s .b) Determine a

A chave mostrada na Figura P7.9 esteve aberta durante um longo tempo, antes de seu fechamento em t = 0 .a) Determine i 0 0 - , i L 0 - e v L 0 - .b) Determine i 0 0 + , i L 0 + e v L 0 + .c) Determine

A chave no circuito da Figura P7.8 esteve fechada por um longo tempo, antes de ser aberta em t = 0 .a) Determine i 1 0 - e i 2 0 - .b) Determine i 1 0 + e i 2 0 + .c) Determine i 1 t para t ≥ 0 .d) De

[a] - Deduza as expressões para as correntes i1(t) e i2(t) para t ≥ 0 . [b] - Use as expressões deduzidas em (a) para determinar i1( ∞ ) e i2( ∞ ).