Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 8

A chave no circuito da Figura P7.8 esteve fechada por um longo tempo, antes de ser aberta em t = 0 .

a) Determine i 1 0 - e i 2 0 - .

b) Determine i 1 0 + e i 2 0 + .

c) Determine i 1 t para t ≥ 0 .

d) Determine i 2 t para t ≥ 0 + .

e) Explique por que i 2 0 - ≠ i 2 0 +

Passo 1

A - Para t

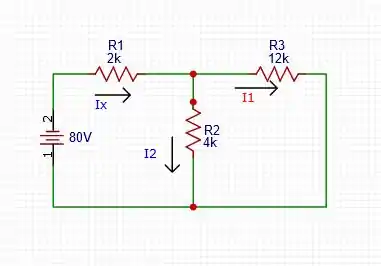
Fazendo paralelo entre os resistores de 4k e 12k, tem-se:

4 k Ω | | 12 k Ω  

4000 × 12000 4000 + 12000 = 3000 Ω   o u   3 k Ω

Para encontrar a corrente que sai da fonte de tensão, tem-se a combinação em série e em paralelo dos resistores, e depois usando a Lei de Ohm ( V = R I ).

I x 0 - = 80 2000 + 3000 = 16   m A

Para encontrar as outras correntes definidas, o divisor de corrente se faz necessário:

I 2 ( 0 - ) = 3000 4000 0.016 = 12   m A

I 1 0 - =   3000 12000 0.016 = 4   m A

Percebeu que a soma das duas correntes I 1 + I 2 é igual a I x , logo, o resultado faz sentido.

Passo 2

B – A corrente no indutor é contínua, portanto:

I 1 0 + = I 1 0 - = 4   m A

Quando a chave abre, haverá uma mudança de sinal, justamente por causa dos sentidos antagônicos dessas duas correntes, logo:

I 2 0 + =   - I 1 0 + =   - 4   m A

Passo 3

C – Para calcular a constante de tempo, temos que pegar a indutância e a resistência equivalente, pela configuração do circuito quando a chave está aberta é:

τ = L e q R e q = 0.64 × 10 - 3 16 × 10 3 = 4 × 10 - 5   s

E o inverso da constante de tempo:

1 τ = 25000

Com isso pode-se ter a equação da corrente:

I 1 t = I 1 0 + e - t / τ

Fazendo a substituição:

I 1 t = 4 e - 25000 t   m A ,     t ≥ 0

Passo 4

D – Nesse caso, tem-se a seguinte relação:

I 2 t =   - I 1 t ,       q u a n d o   t ≥ 0 +

Logo,

I 2 t =   - 4 e - 25000 t   m A ,       t ≥ 0 +

Passo 5

Essa é uma questão bem interessante, vamos analisar. Capacitores e indutores não podem variar instantaneamente tensão e corrente, respectivamente, entretanto o que acontece no resistor?

A questão pede a diferença entre os momentos em que chave abre ou fecha para a corrente I 2 , ok, no resistor a corrente pode mudar instantaneamente, logo, a mudança de estado da chave (de aberto para fechado e vice-versa) força a corrente I 2 0 - = 12   m A e I 2 0 + = - 4   m A .

Resposta

a )   I 1 0 - = 12   m A  

            I 2 0 - =   - 4   m A

b )   I 1 0 + = 4   m A

I 2 0 + =   - 4   m A

c )   I 1 t = 4 e - 25000 t   m A ,     t ≥ 0

d )   I 2 t =   - 4 e - 25000 t   m A ,     t ≥ 0 +

e) A mudança de estado de chave força a corrente de I 2 0 - =   12   m A e I 2 0 + =   - 4   m A

Exercícios de Livros Relacionados

Determine a corrente no indutor para t0 e t0 em cada um dos circuitos da Figura 7.120.
Refaça o Problema 7.17 se i ( 0 ) = 10 A e v ( t ) = 20 u ( t ) V .
Refaça o Problema 7.17 se i ( 0 ) = 10 A e v ( t ) = 20 u ( t ) V .
Determine a resposta ao degrau v o ( t ) para v s = 18 u ( t ) no circuito da Figura 7.124.
Determine v ( t ) para t0 e t0 no circuito da Figura 7.121