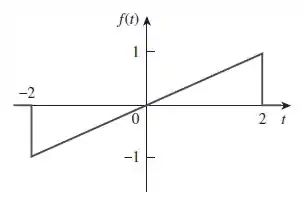
Calcule a transformada de Fourier do sinal na Figura .
Passo 1
Galerinha, podemos expressar essa função da seguinte maneira:
Ou seja, temos um degrau unitário modelado pela função . Vamos aplicar a transformada de Fourier:
Passo 2
Vamos usar a seguinte relação trigonométrica exponencial:
Assim,
Resposta
A transformada é igual a: