Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 5.1 - Ex. 3

Calcule v e i usando o princípio da proporcionalidade.

Passo 1

E aí, galerinha! Oia nós aqui de novo!

Bom! O objetivo aqui é calcular v e i   na Figura do enunciado!

Por isso, antes de mais nada, vamos começar dando nomes aos bois! Isto é, vamo dar uma repaginada bacana nesse circuito...

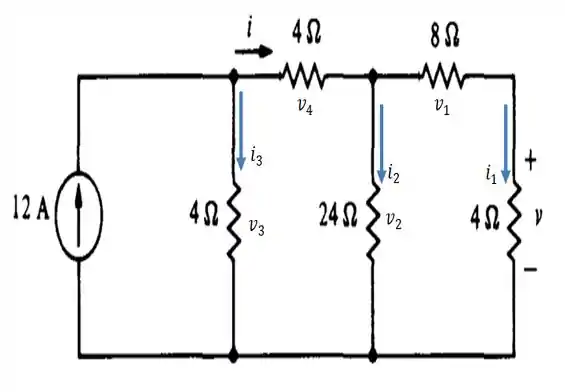
A nossa questão pede pra usar o princípio da proporcionalidade

Por isso, para o nosso propósito, definiremos um elemento linear de maneira mais genérica, que inclui (5.1) como um caso especial. Se x e y são variáveis, tais como tens6es e correntes, associadas com um elemento de dois terminais, então dizemos que o elemento é linear se a multiplicação de x por uma constante K resulta na multiplicação de y pela mesma constante K. Isto é chamado de propriedade da proporcionalidade...

E o nosso circuito aí em cima... De novo! Graças a Deus! É linear!

Vamos então, escolher um elemento e assumir uma tensão para ele... Vamos simplesmente assumir a solução

v = 4   V

Passo 2

Se a tensão v   é de 4   V , então a corrente circulando i 1 vai ser...

i 1 = v 4 = 4 4 = 1   A

E a tensão v 1 então, vai ser dada pelo produto do resistor de 8   Ω por essa corrente i 1

v 1 = 8 i 1

v 1 = 8 ⋅ 1

v 1 = 8   V

Continuando o nosso raciocínio, pelo que podemos ver na figura do enunciado, a tensão v 2 nada mais é do que a soma das tensões v 1 e v :

v 2 = v 1 + v

v 2 = 8 + 4

v 2 = 12   V

Encontrado v 2 , pra achar a corrente i 2 , basta dividir a tensão pela resistência de 24   Ω ...

i 2 = v 2 24 = 12 24 = 0,5   A

Tendo i 2 e também i 1 , pra achar i ... Basta aplicar a L K C :

i = i 1 + i 2

i = 1 + 0,5

i = 1,5   A

Com esse i , pra achar v 4 basta multiplicar a resistência de 4   Ω pela corrente...

v 4 = 4 i

v 4 = 4 ⋅ 1,5 = 6   V

E finalmente, podemos achar v 3 que é nada mais do que a soma de v 4 e v 2 ...

v 3 = v 4 + + v 2

v 3 = 6 + 12

v 3 = 18   V

A corrente i 3 circulando no resistor de 4   Ω será dessa forma, igual à...

i 3 = v 3 4 = 18 4

i 3 = 4,5   A

Isso quer dizer que a fonte de corrente circulando ali sozinha no lado esquerdo do nosso circuito, se assumíssemos que v = 4   V seria igual à...

i c o r r e n t e = i 3 + i

i c o r r e n t e = 4,5 + 1,5

i c o r r e n t e = 6   A

Pronto! Os principais dados já temos aqui!

Passo 3

Pronto! Deu 6   A a nosso fonte de corrente quando usamos a relação v = 4   V ... Só que no enunciado diz que a fonte original é de 12   A !

Ou seja, temos aí uma relação de proporcionalidade igual à...

K = 12 6 = 2

Isso quer dizer que para encontrar os verdadeiros i   e v , basta multiplicar o que encontramos nos passos anteriores por 2 ...

Fazendo isso, obtemos que...

i = 2 ⋅ 1,5

i = 3   A

v = 2 ⋅ 4

v = 8   V

Eureca! Terminamos aqui!

Resposta

i = 3   A

v = 8   V

Exercícios de Livros Relacionados

Se o amp. op. no inversor da Figura 3.14 é não-ideal, como no Prob. 3.31, mostre queV2/V1=(-A(R2/R1))/(A+1+(R2/R1))e então, no caso ideal (A → ∞ ), temos (3.10). Calcule V2/V1 se R2/RI = 2 e A = 10^5
Na Figura 3.3, calcule a resistência vista pela fonte (isto é, olhando pelos terminais a-b)se: a) R 1 = 1,50Ω e R 2 = 2Ω b) R 1 = R 2 = 0,1Ω .
No gráfico do circuito do Problema 4.8, selecione a arvore das fontes de tensão e 0 resistor de 12Ω . Empregando o método desta seção, escreva uma equação da LKC e caIcule v
No gráfico do circuito do Problema 4.8, selecione a arvore das fontes de tensão e o resistor de 12 Ω . Empregando o método desta seção, escreva uma equação da LKC e caIcule v.
Considere o circuito mostrado na Figura P2.17. a) Determine v 0 usando as leis de Kirchhoff e a lei de Ohm. b) Teste a solução para v 0 , verificando que a potência total fornecida é igual à potência