Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.1 - Ex. 4

Calcule o valor de v em regime permanente usando a análise nodal.

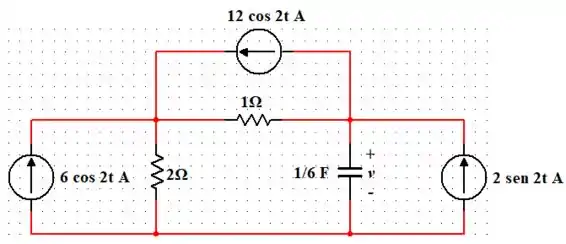
Passo 1

Opaa!! Seguinte... Vamos primeiro passar os valores das fontes para a forma polar e enxergar o capacitor em forma de reatância.

Lembrando que:

X C =   - j ω C

Em que ω = 2   r a d / s .

Logo, temos:

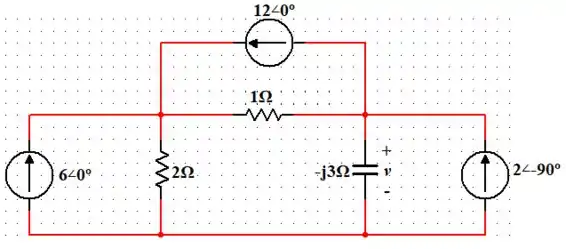
Passo 2

Agora, vamos selecionar os seguintes nós e atribuir direções da corrente e também vamos colocar o terra (referencial de potencial 0 V) na parte de baixo do circuito para facilitar nossa vida:

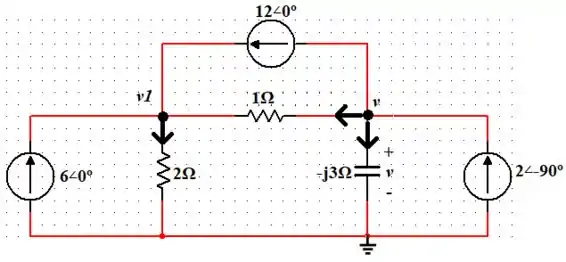
Passo 3

Dessa forma, utilizando a Lei dos Kirchhoff das Correntes no nó v , temos:

2 ∠ - 90 ° = v - v 1 1 + v - j 3 + 12 ∠ 0 ° ∴

- j 2 = v - v 1 + j v 3 + 12 ∴

- j v = 3 v - 3 v 1 + 36 + j 6 ∴

v 3 + j - 3 v 1 = - 3 6 - j 6

Fazendo a meeesma coisa com o nó v 1 :

v 1 2 = 6 ∠ 0 ° + 12 ∠ 0 ° + v - v 1 1 ∴

v 1 2 = 18 + v - v 1 ∴

v 1 = 36 + 2 v - 2 v 1 ∴

2 v - 3 v 1 = - 36

Passo 4

Agora é só resolver esse sistema hehe:

v 3 + j - 3 v 1 = - 36 - j 6 2 v - 3 v 1 = - 36

Resolvendo o sistema pela Regra de Cramer para o sistema 2x2, temos que v é:

v = - 3 6 - j 6 - 3 - 36 - 3 3 + j - 3 2 - 3 ∴

v = 3 2 cos ⁡ 2 t - 135 ° V

Resposta

v = 3 2 cos ⁡ 2 t - 135 ° V

Exercícios de Livros Relacionados

A impedância de um capacitor aumenta com o aumento da frequência.VerdadeiroFalso
Um circuito R L C em série tem R = 30k Ω ,X C = 50Ω e X L = 90Ω . A impedância do circuito é: 30 + j 140Ω 30 + j 40Ω 30 - j 40Ω - 30 - j 40Ω - 30 + j 40Ω
A parte imaginária da impedância é chamada:resistênciaadmitânciasusceptânciacondutânciareatância
Diz-se que uma função que se repete após intervalos fixos é:Um fasorHarmônicaPeriódicaReativa
Qual das seguintes alternativas não é a maneira correta de expressar a senoide A cos ⁡ ( ω t ) ? A cos ⁡ ( 2 π f t ) A cos ⁡ 2 π t T A cos ⁡ w t - T A sin ⁡ ( ω t - 90 ° )