Uma carga industrial cujo modelo é uma associação em série de uma capacitância e uma resistência é mostrada na Figura 9.89. Calcule o valor de um capacitor na associação em série de modo que a impedância resultante seja resistiva em uma frequência igual a
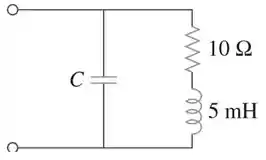
Passo 1
Existem diferentes maneiras de resolver esse problema, mas talvez a maneira mais fácil seja converter os elementos da série em seus equivalentes paralelos. Então tudo que você precisa fazer é fazer com que a indutância e a capacitância se cancelem, resultando em um circuito puramente resistivo.
Ou um resistor de 20 Ohms com um capacitor de !
Passo 2
Para o capacitor, temos que:
E a combinação do capacitor com um indutor é igual a
Agora temos que definir o valor de capacitor, ou seja,