Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 80
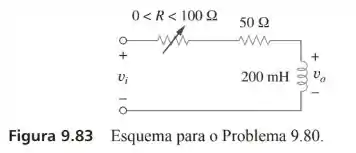
Considere o circuito comutador de fase da figura 9.83. Seja , operando a . Determine:
quando é máxima.
quando é mínima.
O valor de que produzirá um deslocamento de fase igual a .
Passo 1
Primeiramente vamos passar o indutor para impedância e essa conversão é feita a partir da seguinte fórmula
Além disso temos que
Passo 2
Considerando agora o caso em que é máxima vamos ter
Já quando o valor de é mínimo vamos ter
Passo 3
Para obtermos o valor de que produzirá um deslocamento de , a fase de será dada por
Onde para que tenhamos vamos precisar ter
Resposta
Exercícios de Livros Relacionados
A ponte CA mostrada na Figura 9.84 é conhecida como ponte de Maxwell e é usada para medição precisa de indutância e resistência de uma bobina em termos de uma capacitância-padrão Cs. Demonstre que qua
A ponte CA da Figura 9.37 está equilibrada quando R 1 = 400Ω ,R 2 = 600Ω ,R 3 = 1,2k ΩeC 2 = 0,3m F . Determine R x e C x . Suponha que R 2 e C 2 estejam em série.
O circuito CA em ponte da Figura 9.85 e chamada ponte de Wien. Ele é usado para medir a frequência de uma fonte. Demonstre que quando a ponte está equilibrada, f = 1 2 π R 2 R 4 C 2 C 4
O circuito mostrado na Figura 9.86 é usado em um televisor. Qual é a impedância total desse circuito?
Um circuito de áudio em série é apresentado na Figura 9.88.Qual é a impedância?Se a frequência for dividida pela metade, qual seria a impedância do circuito?