Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 71
Para o circuito com amplificador operacional da Figura 7.136, suponha = 0 e = 3 V. Determine v(t) para t > 0.
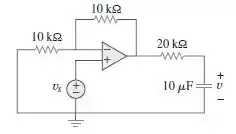
Passo 1
Para resolver este circuito precisamos primeiro encontrar o equivalente de Thevenin nos terminais do capacitor, assim devemos remover o capacitor e considerar o circuito aberto para achar De tal modo que,
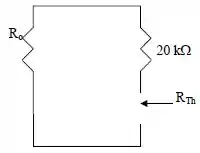
Passo 2
Como estamos assumindo um amplificador operacional ideal, temos que
Como trata-se de um amplificador operacional não inversor, sabemos que,
Ou seja,
Desse modo o equivalente de Thevenin é:
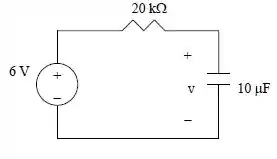
Passo 3
Agora que já sabemos o circuito equivalente, podemos calcular v(t) do jeito que aprendemos. Assim a constante de tempo é:
Substituindo na eq,
Temos,