Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 63

Para o circuito com amplificador operacional da Figura 8.108 , detemrine a equação diferencial para i ( t ) .

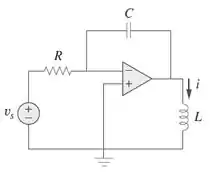
Passo 1

Galera, vamos assumir aqui que nosso amp-op é ideal, beleza? Assim, podemos assumir o seguinte:

i - = i + = 0 … 1

v - = v + … ( 2 )

Onde:

  • i + : é a corrente no terminal não-inversor;
  • i - : é a corrente no terminal inversor;
  • v + : é a tensão no nó não-inversor;
  • v - : é a tensão no nó inversor.

Passo 2

Vamos aplicar a análise nodal no nó inversor v - :

v - - v s R + i c + i - = 0

Onde i C é a corrente que passa pelo capacitor e, de ( 1 ) e ( 2 ) , temos:

i - = 0

v - = v +

Como v + está conectado à terra, logo v + = 0 . Isso nos leva a:

- v s R + i C = 0 … ( 3 )

Passo 3

A corrente que passa pelo capacitor i C é dada por:

i C = C d v c d t … ( 4 )

Onde v C é a tensão no capacitor. Do circuito, podemos tirar a seguinte relação entre tensões:

v C = v - - v L

Onde v L é a tensão no indutor. Além disso,

v C = - v L = - L d i d t

d v C d t = - L d 2 i d t 2

Substituindo na equação ( 4 ) ,

i C = - L C d 2 i d t … ( 5 )

Passo 4

Se substituirmos a equação ( 5 ) em ( 3 ) , teremos:

- v s R - L C d 2 i d t = 0

L C d 2 i d t = - v S R

d 2 i d t = - v S R L C

Resposta

A equação é igual a:

d 2 i d t = - v S R L C

Ver Outros Exercícios desse livro