Determine a equação diferencial para o circuito com AOP da Figura . Se e , determine para . Seja e .
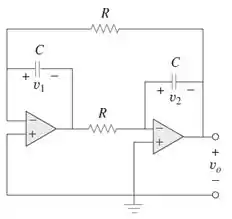
Passo 1
Galera, vamos assumir aqui que os nossos amp-ops são ideais, beleza? Assim, podemos assumir o seguinte:
Para o segundo amplificador:
Onde:
- : é a corrente no terminal não-inversor;
- é a corrente no terminal inversor;
- : é a tensão no nó não-inversor;
- : é a tensão no nó inversor.
Passo 2
Da figura, podemos concluir que
Usando a lei dos nós no nó não inversor do primeiro amplificador operacional, temos:
Usando a lei dos nós no nós não inverso do segundo amplificador, temos:
Derivando a equação em relação a , temos:
Substituindo e em :
Dividindo a equação por e reorganizando seus termos:
Passo 3
A equação característica pode ser escrita como:
Com as raízes sendo
O sistema é amortecido supercrítico e é dado por:
Sabendo que ,
Da equação :
Passo 4
Derivando a equação :
Substituindo na equação
Substituindo os valores de e na equação, temos:
Sabemos que
Das equações e , podemos concluir que
Logo,
Resposta
A tensão é igual a: