Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 69
Para o circuito com AOP da Figura 7.134, determine vo(t) para t > 0.
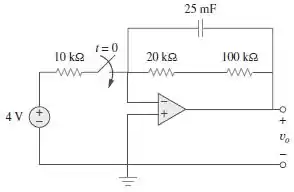
Passo 1
Primeiro vamos relembrar o que é o amplificador operacional. Nada mais é que um seguidor de tensão, ou seja,
Antes de continuar vamos numerar o nó entre os resistores de 10 e 20 de nó 1.
Passo 2
Certo! Agora vamos analisar depois que a chave fecha, ou seja, para t>0. Note que os resistores de 20 e 100 estão em series e o capacitor pode ser tratado como circuito aberto.
Assim,
Para note que a tensão no nó 1 e igual a 0, portanto a corrente que passa pelo resistor de 10k é:
E como a corrente não passa pelo capacitor por estar em circuito aberto e para o amplificador operacional, o único caminho é pelos resistores, logo
Passo 3
Substituindo na equação abaixo teremos,