Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 47

Determine v ( t ) para t > 0 no circuito da Figura 7.114 se v (0) = 0 .

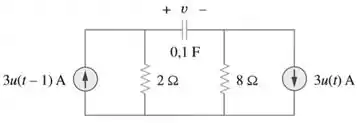
Passo 1

Okay galera, essa questão tem um circuito nem tão básico, mas vamos definir em 3 momentos: Antes do t = 0 , 0 < t < 1 e t > 1 . Então, bora lá!

Para t < 0 ,

u (t) = 0 , u (t - 1) = 0 , v (0) = 0

Para 0 < t < 1 ,

tau = R C = (2 + 8) (0.1) = 1

v (0) = 0 , v (oo) = (8) (3) = 24

v (t) = v (oo) + [v (0) - v (oo)] e^(- t // tau)

v (t) = 24 ( 1 - e^(- t) )

Para t > 1 ,

v (1) = 24 (1 - e^(- 1)) = 15.17

- 6 + v (oo) - 24 = 0 -> v (oo) = 30

v (t) = 30 + (15.17 - 30) e^(- ( t - 1 ))

v (t) = 30 - 14.83 e^(- ( t - 1 ))

Passo 2

Organizando, temos que:

v (t) = {[[24 (1 - e^(- t)) V , 0 < t < 1],[30 - 14.83 e^(- (t - 1)) V , t > 1]])

Resposta

v (t) = {[[24 (1 - e^(- t)) V , 0 < t < 1],[30 - 14.83 e^(- (t - 1)) V , t > 1]])

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a entrada para um sistema linear for δ ( t ) e a saída e - 2 t u ( t ) , a função de transferência do sistema será:a) 1 s + 2 b) 1 s - 2 c) s s + 2 d) s s - 2
A corrente através de um circuito R L em série com tensão de entrada v ( t ) é dada no domínio s como:a) V s R + 1 s L b) V ( s ) ( R + s L ) c) V s R + 1 s L d) V s R + s L
A impedância de um capacitor de 10F é:a) 10 s b) s 10 c) 1 10 s d) 10 s
Um sistema com única entrada e única saída é descrito pelo modelo de estados a seguir: x 1 = 2 x 1 - x 2 + 3 z x 2 = - 4 x 2 - z y = 3 x 1 - 2 x 2 + z Qual das matrizes seguintes é incorreta?a) A = 2
Qual das seguintes equações é denominada equação de estados?a) x = A x + B z b) y = C x + D z c) H s = Y ( s ) / Z ( s ) d) H s = C s I - A - 1 B