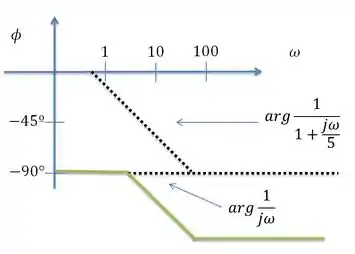
Elabore um problema para ajudar outros estudantes a entender melhor como determinar os gráficos de bode de amplitude e de fase de uma função de transferência em termos de
Passo 1
Faça o esboço do gráfico de Bode da amplitude e da fase da seguinte função de transferência
Passo 2
Primeiramente vamos colocar a função de transferência na forma padrão de polos e zeros, dividindo em cima e embaixo por
Assim possuímos três fatores na função de transferência são eles
O ganho
O fator com polo simples e frequência de corte em
E outro fator com polo simples e frequência de corte em
Passo 3
O gráfico de bode pode ser feito parte a parte ou fator a fator. Assim vamos começar pelo fator
Este tem modulo e fase. Mas para ser posto no gráfico de bode a amplitude tem que estar em decibel, logo
Que é igual a
Logo no gráfico ficará
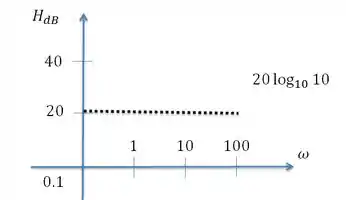
A fase do fator constante é igual a zero
Passo 4
Com adição do fator o gráfico de fase fica

E o gráfico de fase fica

Resposta
Com adição do fator final o gráfico ficará
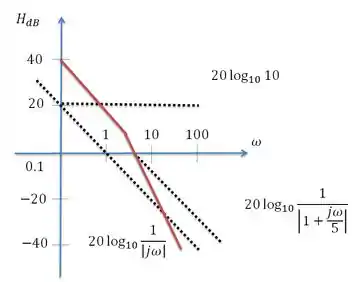
E o gráfico de fase será