Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 17

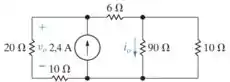
Para o circuito divisor de corrente da Figura 3.17, calcule:

a) i o e v o .b) a potência dissipada no resistor de 6 Ω .c) a potência fornecida pela fonte de corrente.

Passo 1

Fala, galera! Beleza? Espero que sim. Bora resolver uma questão bem legal hoje!

a) Primeiramente desejamos achar a resistência equivalente para poder achar a tensão entre os pontos da fonte de corrente.

R e q = ( 90 10 + 6 30 = 9 + 6 30 = 15 | | 30 = 10 Ω

Ou seja, nós temos um resistência de 10 Ω em paralelo com a fonte de corrente de 2,4 A.

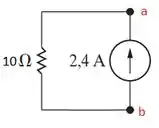
Usando que V=RI, temos:

v a b = 2,4 ⋅ R e q = 2,4 ⋅ 10 = 24 V

Passo 2

Se v a b = 24 V , usando isso diretamente no desenho original, nós temos um resistor de 30 Ω sob essa ddp de 24V, então, podemos encontrar a corrente que passa ali no lado esquerdo do circuito.

i l = v a b 30   = 24 30 = 0,8 A

Fazendo que v o = i l ⋅ 20 = 0,8 ⋅ 20

v o = 16 V

Já para a corrente i o , podemos usar o divisor de tensão diretamente:

v 90 Ω = v a b ⋅ R e R e + 6      

Onde R e = 90 | | 10 = 9 Ω

Logo:

v 90 Ω = 24 ⋅ 9 15 = 14,4 V

Agora podemos facilmente encontrar i o :

v 90 Ω = i o ⋅ R 90

14,4 = i o ⋅ 90  

i o = 0,16 A

Passo 3

b. A potência no resistor de 6 Ω pode ser calculado usando P = V 2 R .

Onde V = v a b - v 90 Ω = 24 - 14,4 = 9,6 V  

Logo:

P = 9,6 2 6 = 15,36 W

c. A potência ser fornecida quer dizer que o sinal é negativo. Logo, podemos fazer que P = VI.

P f o n t e = - 2,4 ⋅ 24 = - 57,6 W

Resposta

a. i o = 0,16 A

b. P = 15,36 W  

c. P f o n t e = - 57,6 W

Exercícios de Livros Relacionados

Um voltímetro de d’Arsonval é mostrado na Figura. Determine o valor de Rv para cada uma das seguintes leituras máximas: (a)50 V, (b) 5 V, (c) 250 mV e (d) 25 mV.
Calcule v .
Calcule i_1 , i_2 e v .
Calcule i .
Calcule i e v_a b .