Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 37

Um voltímetro de d’Arsonval é mostrado na Figura. Determine o valor de Rv para cada uma das seguintes leituras máximas: (a)50 V, (b) 5 V, (c) 250 mV e (d) 25 mV.

Passo 1

Falaa, galera!! Beleza? Bora para mais uma questão de circuitos elétricos.

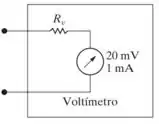
Primeiramente iremos calcular a resistência do medidor.

R m e d i d o r = 20 m V 1 m A = 20 Ω

Logo, temos que:

R m e d i d o r + R v = V d e s e j a d a 10 - 3

R v = 1000 ⋅ V d e s e j a d a - 20

Passo 2

Agora podemos usar essa equação para cada caso:

a) V d e s e j a d a = 50 V

R v = 1000 ⋅ 50 - 20 = 49,980 Ω

b) V d e s e j a d a = 5 V

R v = 1000 ⋅ 5 - 20 = 4980 Ω

Passo 3

c) V d e s e j a d a = 250 m V

R v = 1000 ⋅ 250 m - 20 = 230 Ω

d) V d e s e j a d a = 25 m V

R v = 1000 ⋅ 25 m - 20 = 5 Ω

Resposta

a)49,980 Ω

b)4980 Ω

c)230 Ω

d)5 Ω

Exercícios de Livros Relacionados

Calcule i e a potência entregue ao resistor de 4Ω.
Projete um divisor de tensão que forneça 2, 6, 10, 24 e 40 V, referente a um terminal negativo comum, a partir de uma fonte de 50 V, que fornece 100 mW de potência.
Calcule todas as tensões de saída possíveis, inferiores a 14 V, que podem ser obtidas pela construção de divisores de tensão com uma fonte de 14 V em série com três resistores cujos valores são, respe
Projete um divisor de tensão que forneça 4, 10 e 20 V, referente a um terminal negativo comum, a partir de uma fonte de 25 V. A fonte fornece 25 mW de potência.
Calcule i , v a b e um circuito equivalente para i contendo uma única fonte e um único resistor.