Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 47
Para o circuito da figura 6.70, calcule o valor de que fará a energia armazenada no capacitor ser a mesma que aquela armazenada no indutor em CC.
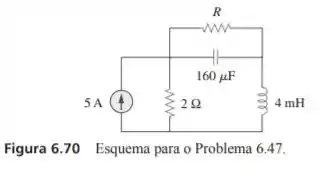
Passo 1
Sob as condições de corrente contínua (CC) nós vamos reescrever o circuito como sendo
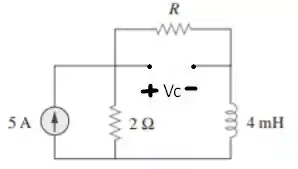
Primeiramente vamos aplicar as condições de divisor de corrente e a lei de Ohm para , vamos encontrar, assim,
Passo 2
Agora, para a energia armazenada no capacitor e no indutor vamos ter
Por fim, devemos descobrir o valor de que fará a energia armazenada no capacitor e no indutor ser a mesma basta igualar os valores de e então encontraremos
Resposta
Exercícios de Livros Relacionados
Indutores em paralelo podem ser associados da mesma forma que resistores em paralelo.VerdadeiroFalso
Se a corrente através de um indutor e 10 mH aumenta de zero a 2 A, qual é a quantidade de energia armazenada no indutor??40 mJ20 mJ 10 mJ5 mJ
Um capacitor de 4mF apresenta a seguinte tensão em seus terminais. v =50V ,t ≤ 0 Ae - 100 t + B e - 600 t ,t ≥ 0 Se o capacitor tiver uma corrente inicial de 2A, determine a energia armazenada no capa
Em t=0, a tensão em um capacitor de 25 mF é 10 V. Calcule a tensão do capacitor para t0 quando a corrente 5t mA passa através dele.
Um capacitor de 4mF apresenta a seguinte tensão em seus terminais. v =50V ,t ≤ 0 Ae - 100 t + B e - 600 t ,t ≥ 0 Se o capacitor tiver uma corrente inicial de 2A, determine as constantes A e B.