Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 60

No circuito da figura 6.82, i_o (0) = 2 A . Determine i_0 (t) e v_0 (t) para t > 0 .

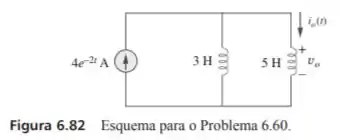
Passo 1

Para facilitar e ajudar nossa análise devemos observar que os dois indutores estão associados de forma paralela e, portanto, sua indutância equivalente será dada por

L_e q = (3 * 5)/(3 + 5) = (15)/(8)

Assim, conseguimos equacionar v_0 fazendo

v_0 = L_e q * (d i)/(d t) = (15)/(8) * (d (4 e^(- 2 t)))/(d t) = - 15 e^(- 2 t)

Por fim, conseguimos calcular i_0 (t) já que obtemos v_0 (t) basta fazermos

i_0 = (1)/(L) * int_0^t v_0 (t) d t + i_o (0) = [2 + (3)/(2) * e^(- 2 t)]_0^t = 0.5 + 1.5 * e^(- 2 t) A

Resposta

v_0 (t) = - 15 e^(- 2 t) , i_0 (t) = 0.5 + 1.5 e^(- 2 t)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Supondo que os capacitores estejam inicialmente descarregados, determine Vo(t) no circuito da figura abaixo.
A corrente através de um indutor de 10 mH é 10 e - t / 2A . Determine a tensão e a potência em t=3s.
Dado que quatro capacitores de 4μ F podem ser conectados em série e em paralelo, calcule os valores máximo e mínimo que podem ser obtidos por tais associações série-paralelo.
Obtenha a capacitância equivalente do circuito da figura abaixo.
Se V(0) = 0, determine V(t), i1 (t) e i2(t) no circuito da figura abaixo.