No circuito da Figura 7.140, determine e, dado que = 4u(t) V e v(0) = 1 V.
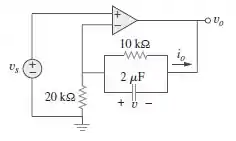
Passo 1
Pela a informação que a questão nos oferece sabemos que,
Para t>0
Passo 2
Observe que,
Note que, também pode ser expresso pela soma de duas correntes a que passa pelo capacitor e pelo resistor . Desse modo,
Substituindo a primeira equação
Sabemos que a solução para essa equação diferencial é dada por
Passo 3
É evidente que,
A questão nos oferece que,
E quando tende ao infinito o capacitor pode ser tratado como circuito aberto, portanto a equação
Torna
Resolvendo
Substituindo, temos
Passo 4
Porém a questão nos pede a tensão , mas sabemos que,
Ou seja
Quase terminando! Não vamos esquecer do , sabemos que,