Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas Abrangentes - Ex. 90
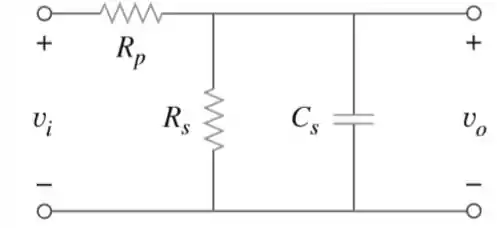
Uma ponta de prova de atenuação empregada em osciloscópios foi projetada para reduzir a magnitude da tensão de entrada vi por um fator 10. Conforme ilustrado na Figura 7.149, o osciloscópio possui resistência interna e capacitância , enquanto a ponta de prova tem resistência interna . Se for fixa em , determine e para o circuito ter uma constante de tempo igual a .
Passo 1
Uhuul! Vamo pra cima! Primeiro, vamos determinar o equivalente de Thevenin de circuito para o capacitor .
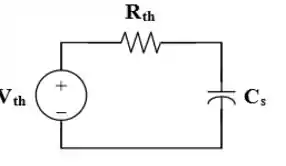
O equivalente de Thevenin é um circuito RC, logo
Passo 2
Legal! Agora temos que:
Onde,
Resposta
Exercícios de Livros Relacionados
A chave no circuito da Figura P7.80 esteve na posição a por um longo tempo. EM t=0, ela passa instantaneamente para a posição b, onde permanece por 5 segundos antes de passar instantaneamente para a p
A chave no circuito da Figura P7.88 esteve fechada por um longo tempo. A tensão máxima nominal do capacitor de 1,6 mF é 14,4 kV. Em quanto tempo, depois da abertura da chave, a tensão no capacitor alc
A forma de onda de tensão mostrada na Figura P7.84 (a) é aplicada ao circuito da Figura P7.84(b). A corrente inicial no capacitor é igual a zero.Calcule v 0 ( t ) .Faça um gráfico de v 0 t em função d
A fonte de tensão no circuito da Figura P7.83(a) está gerando o sinal mostrado na Figura P7.83(b). Não há nenhuma energia armazenada em t=0.Determine as expressões para v 0 ( t ) que sejam válidas par