Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 3

Para o circuito mostrado na Figura 14.70, R 1 = 2   Ω , R 2 = 5   Ω , C 1 = 0,1   F e C 2 = 0,2   F , determine a função de transferência H s = V 0 ( s ) / V i ( s )

Passo 1

Vamos lá para mais um problema de função de transferência

Para resolvê-lo vamos passar o circuito para o domínio da frequência, para isso os componentes devem ser trocados por suas respectivas impedâncias.

O resistor como não varia com a frequência tem seu valor inalterado. Já a impedância capacitiva dependente da frequência, logo:

R 1 = 2   Ω

R 2 = 5   Ω

0.2 F → X c 1 = 1 j ω C = 1 s ( 0.2 ) = 5 s Ω

0.1 F → X c 2 = 1 j ω C = 1 s ( 0.1 ) = 10 s Ω

Ficando com o circuito da seguinte forma

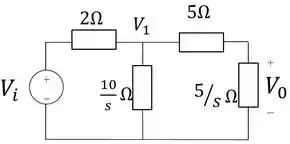
Passo 2

Jovin!! Seguinte!!

Para determinar a função de transferência vamos precisar da variável de entrada V i e a variável de saída V 0 .

Para isso devemos simplificar este circuito. Como trata-se de impedâncias podemos somar a impedância do resistor R 2 com a impedância do capacitor X c 2 .

Chamaremos essa associação de Z 1

Z 1 = 5 + 5 s

Ficando com

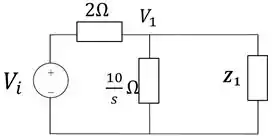
Passo 3

Em seguida tiraremos o paralelo entre a impedância X c 1 e Z 1 , para encontrar Z

Z = X c 1 / / Z 1     = 10 s / / 5 + 5 s  

Multiplicando em cima e somando embaixo,

Z =     10 s ⋅ 5 + 5 s 5 + 15 s

Colocando 5 em evidência no numerador e 5 s no denominador, teremos

Z = 10 s 5 1 + 5 s 5 s ( 3 + s ) = 10 s + 1 s s + 3

Simplificando o 5 s que temos no numerador e no denominador obteremos Z igual a

Z = 10 s + 1 s s + 3

Resultando no circuito

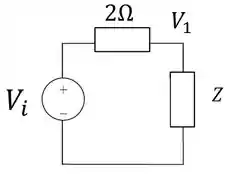
Passo 4

Agora que temos Z podemos encontrar V 1 pelo divisor de tensão

V 1 = Z Z + 2 ⋅ V i

Te liga que o V i apareceu ali. Mas segura a emoção, estamos quase no fim.

Passo 5

Vê se tu concordas comigo. A tensão de saída é a tensão sobre a impedância X c 2 desta maneira teremos que aplicar novamente um divisor de tensão.

V 0 = 5 / s 5 + 5 / s ⋅ V 1 = 5 5 s + 5   ⋅ V 1 =   1 s + 1   ⋅ V 1  

Mas V 1 já temos, basta substituir.

V 0 = 1 s + 1 ⋅ Z Z + 2 ⋅ V i

Passo 6

Daqui é só partir pro abraço.

H s = V 0 V i = 1 ( s + 1 ) ⋅ 10 s + 1   s s + 3 2 + 10 s + 1 s s + 3 = 10 s + 1   s s + 3 s + 1 ⋅ [ 2 s s + 3 + 10 s + 1 ]

Dividindo o numerador e o denominador por ( s + 1 )

H s = 10 2 s s + 3 + 10 s + 1

Fazendo a distributiva do denominador

H s = 10 2 s 2 + 6 s + 10 s + 10 = 10 2 s 2 + 16 s + 10

Dividindo por 2 em cima embaixo

H s = 5 s s 2 + 8 s + 5

Resposta

A função de transferência é

H s = 5 s s 2 + 8 s + 5

Ver Outros Exercícios desse livro