Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 6
Considere o circuito mostrado na Figura 14.73 e determine
Passo 1
Neste problema a função de transferência trata-se de um ganho de corrente. Pois como podemos ver a variável de saída é a corrente e a variável de entrada é a corrente
Para darmos inicio teremos que pensar nos componentes em termos de suas impedâncias, para que o circuito possa ser analisado no regime de frequência.
Passo 2
Vamos pegar um caminho que você vai logo entender o pq. O caminho da tensão
A tensão que está sobre o indutor é a mesma que esta sobre o resistor , para simplificação vamos tirar o equivalente entre o paralelo de e chamado de
Dividindo por 2 em cima e embaixo
Ficando com
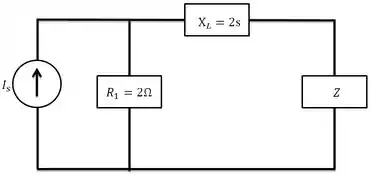
Passo 3
Vamos agora transformar a fonte de corrente em uma fonte de tensão. E obtermos
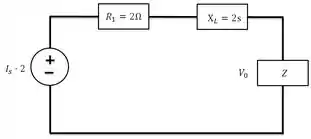
Passo 4
Para conseguir o valor da tensão precisamos recorres ao divisor de tensão, pois a corrente sobre o circuito agora é a mesma, porem a tensão não. Para isso faremos
Substituindo
Colocando todos no mesmo denominador
Simplificando o
Simplificando por
Passo 5
Uma vez que a tensão sobre é a mesma tensão sobre o resistor no qual passa a corrente poderemos fazer a relação
E, portanto a função de transferência será.
Resposta
A função de transferência é