Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 23
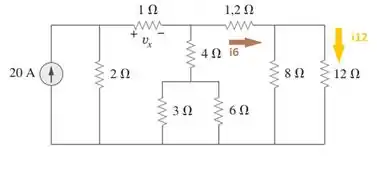
No circuito mostrado na figura , determine e a potência absorvida pelo resistor de .
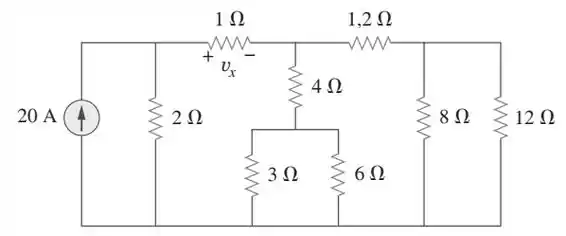
Passo 1
Bora lá! Dá uma olhadinha nesse circuito.
Vamos arrumar essas resistências! Na parte laranja, os resistores de e estão em paralelo, e depois, em série com o de . Isso vai resultar:
Na parte azul, também temos um paralelo dos resistores de e , em série com o de .
E essas duas partes também estão em paralelo entre si, como mostra a figura a seguir:
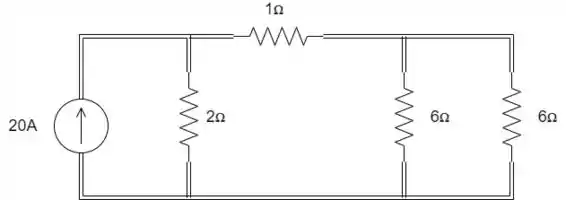
Passo 2
Colocando os dois resistores de em paralelo, teremos uma resistência equivalente igual a:
Então percebemos que os resistores de e estão em série. Nosso circuito fica então da seguinte forma:
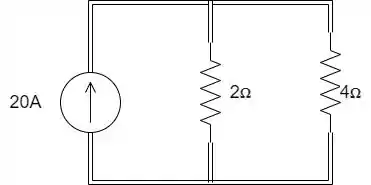
Passo 3
A corrente de vai se dividir nesses dois lados: pro de e pro de .
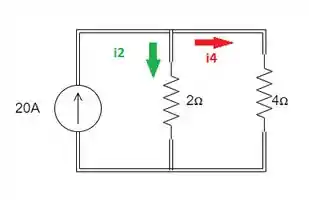
Assim, podemos utilizar um divisor de corrente, utilizando a fórmula:
Aplicando nos resistores que nós temos:
Enquanto:
Passo 4
Essa é a corrente que vai passar no resistor de , então sua tensão será:
Passo 5
Depois de passar pelo resistor de , ela vai se dividir nesses dois ramos.
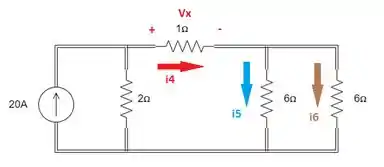
Como os dois têm a mesma resistência equivalente de , a corrente vai se dividir igualmente em duas de :
Depois, a corrente se divide finalmente nos resistores de e .
Como estão em paralelo, vamos usar o divisor de corrente novamente para encontrar a corrente que passa pelo resistor de :
Aplicando os nossos valores:
Passo 6
E portanto, a potência absorvida por ele é definida pela fórmula: