Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 64

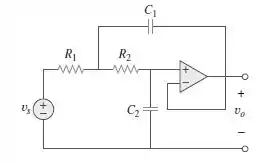
Considera a Figura 8.109 e elabore um problema para ajudar outros estudantes a entenderem melhor os circuitos de segunda ordem com AOP.

Passo 1

Vamos resolver o seguinte problema:

“Para o circuito dado, encontre a expressão para v 0 ( t ) , com os seguintes parâmetros: R 1 = R 2 = 1   Ω ,   C 1 = 1   F ,   C 2 = 2   F ,   v S = 10   V .”

Bom, pessoal, para t → ∞ , precisamos determinar as condições de regime permanente. Os capacitores atuam como um circuito aberto. Assim, a tensão de saída é igual a:

v 0 ∞ = v s = 10   V

Passo 2

Dois nós serão utilizados para analisar o circuito: nó (a), que está entre R 1 e R 2 e nó (b), no terminal positivo do capacitor. Para encontrarmos a resposta transiente, vamos aplicar a lei das malhas e dos nós em ambos os nós.

A tensão v 0 ( t ) é dada por:

v 0 t = v a t - v b t … 1

Aplicando a lei dos nós no nó a:

v s - v a R 1 = C 2 d v b d t + v a - v 0 R 2 … ( 2 )

Aplicando, também, a lei dos nós no nó b:

v a - v 0 R 2 = C 1 d v 0 d t … ( 3 )

Passo 3

Se derivarmos a equação ( 1 ) , teremos:

d v 0 d t = d v 0 d t - d v b d t

d v b d t = d v a d t - d v 0 d t … 4

Substituindo a equação ( 3 ) em ( 2 ) :

v s - v a R 1 = C 2 d v b d t + C 1 d v 0 d t … ( 5 )

Substituindo a equação ( 4 ) em ( 5 ) :

v s - v a R 1 = C 2 d v a d t - d v 0 d t + C 1 d v 0 d t

v s - v a R 1 = C 2 d v a d t - C 2 d v 0 d t + C 1 d v 0 d t … 6

Passo 4

Da Equação ( 3 ) , nós podemos tirar que:

v a = R 2 C 1 d v 0 d t + v 0 R 2 … 7

Derivando a equação ( 7 ) em relação a t ,

d v a d t = R 2 C 1 d 2 v 0 d t 2 + 1 R 2 d v 0 d t … ( 8 )

Substituindo as equações ( 7 ) e ( 8 ) em ( 6 ) , temos:

v s R 1 - R 2 R 1 C 1 d v 0 d t + v 0 R 2 = C 2 R 2 C 1 d 2 v 0 d t 2 + 1 R 2 d v 0 d t - C 2 d v 0 d t + C 1 d v 0 d t … ( 9 )

Vamos substituir os valores de R 1 ,   R 2 ,   C 1 e C 2 :

v S - d v 0 d t + v 0 = 2 d 2 v 0 d t 2 + d v 0 d t - 2 d v 0 d t + d v 0 d t

Reorganizando os termos da equação:

d 2 v 0 d t 2 + 2 d v 0 d t + v 0 = v s … ( 10 )

A equação característica é igual a:

s 2 + 2 s + 1 = 0

As raízes da equação característica são:

s 1,2 = - 1 2 ± 1 2 j

Disso, podemos tirar que α = 1 2 e ω d = 1 2 . Precisamos, agora, achar o valor de ω 0 .

ω 0 = α 2 + ω d 2 = 1 2 2 + 1 2 2 = 2 2   r a d / s

Isso nos leva a α < ω 0 , que caracteriza a resposta do circuito como subamortecida. Assim, a resposta transiente é dada por:

v t t = A 1 cos ⁡ ω d t + A 2 sin ⁡ ω d t e - α t

Assim, finalmente (!!!!), a solução completa é dada por:

v 0 t = v 0 ∞ + v t t = 10 + A 1 cos ⁡ ω d t + A 2 sin ⁡ ω d t e - α t

v 0 t = 10 + A 1 cos ⁡ 0,5 t e - 0,5 t + A 2 sin ⁡ 0,5 t e - 0,5 t

Resposta

A tensão v 0 ( t ) é igual a:

v 0 t = 10 + A 1 cos ⁡ 0,5 t e - 0,5 t + A 2 sin ⁡ 0,5 t e - 0,5 t

Ver Outros Exercícios desse livro