Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 46

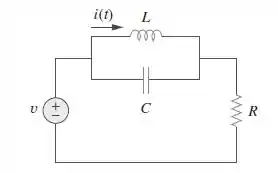
Usando a Figura , elabore um problema para ajudar outros estudantes a entenderem melhor a resposta a um degrau de um circuito em paralelo.

Passo 1

Galerinha, vamos lá. Para fazer essa questão seria interessante atribuirmos valores para cara um dos componentes no circuito. Seja a fonte de tensão gerando , o capacitor de , o indutor com e o resistor com . A primeira coisa que podemos fazer é transformar esse circuito em um RLC paralelo. Para isso, vamos realizar uma transformação de fonte, fazendo essa fonte de tensão em série com o resistor virar uma fonte de corrente em paralelo com o resistor. Assim, temos

Assim, o nosso circuito passa a ser:

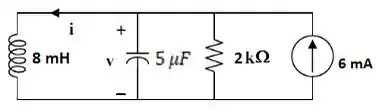
Para o instante , , logo, e .

Passo 2

A próxima coisa que podemos começar a fazer é analisar os valores de e e achar as raízes características:

Como temos que , a resposta do circuito é subamortecida. Assim,

Portanto, a equação da nossa corrente será da forma:

Para o instante inicial , o enunciado já nos forneceu o valor da corrente! Assim, substituindo na expressão acima , obtemos:

A mesma análise inicial também foi feita para a tensão. Sabemos que, em , . Como temos nossos três elementos do circuito em paralelo, todos eles estão sob a mesma tensão, ou seja