Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 55
Considere a Figura 11.74 e elabore um problema para ajudar outros estudantes a entender melhor a conservação de potência CA
Passo 1
Esse é daqueles exercícios onde podemos colocar qualquer valor para os componentes dados no circuito. Então se colocarmos:
E quisermos calcular a potência total em todos os componentes nós teremos:
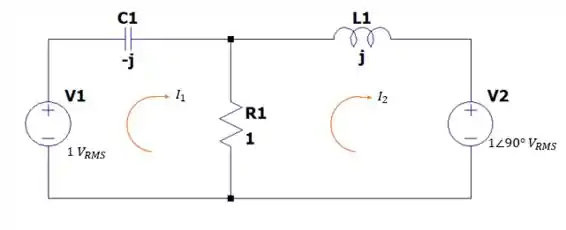
Na malha 1 (onde passa a corrente ) temos a seguinte somatória de tensões:
Ou:
Agora as tensões na malha (onde corre a corrente ):
Pois a corrente entra na fonte nos dando uma tensão negativa (se olharmos pro sentido da corrente)
Passo 2
Resolvendo o sistema abaixo teremos:
E com isso podemos resolver as potências totais de todos os componentes:
Então a potência que sai das fontes serão:
Não se esquecendo que a potência que entra na fonte é negativa pois a corrente entra na fonte.
Portanto
E a potência total em cada elemento passivo será:
Somando todas as potências nos elementos nós teremos:
E a afirmação nos diz que há a conservação da potência no circuito. Mesmo que ela seja em corrente alternada.