Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 8

Considere a Figura 17.51 e elabore um problema para ajudar outros estudantes a entender melhor como determinar a série de Fourier exponencial de uma forma de onda periódica.

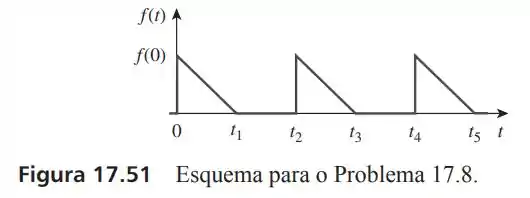
Passo 1

Vamos considerar f 0 = 5 e t 1 = 1 , t 2 = 2 , t 3 = 3 , … e por aí vai isso faz com que o período dessa onda periódica seja:

T = 2

Pois é quando temos a reta vertical de 0   até 5 , portanto a velocidade angular da onda será:

ω = 2 π T = π

E aí podemos dividir a onda no período de 0 < t < 2   em duas partes:

f t = 5 - 5 t ,     0 < t < 1 0 ,     1 < t < 2

E uma função periódica na forma exponencia tem que estar na forma:

f t = ∑ n = - ∞ ∞ c n e j n ω 0 t

Onde:

c n = 1 T ∫ 0 T f t e - j n ω 0 t d t  

Passo 2

Então fazendo a conta para c n nós temos (para ω 0 = π ):

c n = 1 2 ∫ 0 1 5 1 - t e - j n π t d t + 0

Já que no intervalo de 1 < t < 2 a função f ( t ) é nula, então nossa integral pode ser escrita como:

c n = 5 2 ∫ 0 1 e - j n π t d t - ∫ 0 1 t e - j n π t d t

Onde ∫ e a t = 1 a e a t + c , logo ∫ e - j n π t = 1 - j n π e - j n π t e no apêndice C seção C . 5 desse livro temos que a integral por partes da função ∫ x e a x d x = e a x a 2 a x - 1 + c

Portanto:

∫ t e - j n π t d t = e - j n π t j 2 n 2 π 2 - j n π t - 1

Aplicando o intervalo de 0 até 1 teremos:

c n = 5 2 e - j n π t - j n π 0 1 - e - j n π t j 2 n 2 π 2 - j n π t - 1 0 1

c n = 5 2 e - j n π - 1 - j n π - e - j n π - n 2 π 2 - j n π - 1 - 1 - n 2 π 2 - 1

Arrumando os sinais

c n = 5 2 1 - e - j n π j n π + e - j n π n 2 π 2 - j n π - 1 + 1 n 2 π 2

Só que temos uma relação trigonométrica com o número de Euler extremamente importante que é:

e j θ = cos ⁡ θ + j s e n   θ

Portanto:

e - j n π = cos ⁡ - n π + j s e n ( - n π )

Só que por ser uma função par o cosseno ficará cos ⁡ - n π = c o s ⁡ ( n π ) e por n ser um número inteiro n = 1,2 , 3 , … então s e n ( n π ) sempre será nulo. Portanto:

e - j n π = cos ⁡ n π = ( - 1 n )

Tal como pode ser visto na tabela 17.1 desse livro ( q u i n t a   e d i ç ã o )

Portanto c n fica sendo escrito como:

c n = 5 2 1 - ( - 1 n ) j n π + ( - 1 n ) n 2 π 2 - j n π - 1 + 1 n 2 π 2

E a série de Fourier na forma exponencial fica:

f t = ∑ n = - ∞ ∞ 5 2 1 - ( - 1 n ) j n π + ( - 1 n ) n 2 π 2 - j n π - 1 + 1 n 2 π 2 e j n π t

Resposta

f t = ∑ n = - ∞ ∞ 5 2 1 - ( - 1 n ) j n π + ( - 1 n ) n 2 π 2 - j n π - 1 + 1 n 2 π 2 e j n π t

Ver Outros Exercícios desse livro