Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 2
Considere a Figura 14.69 e elabore um problema para ajudar outros estudantes a entender melhor como determinar funções de transferência.
Passo 1
A figura 14.69 apresenta o circuito
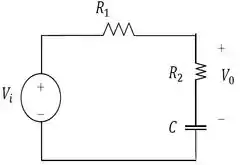
O Problema nos deu liberdade para criar uma forma de entender como obter a função de transferência.
Antes de tudo teremos que lembrar que a função de transferência é uma relação que explica o sistema (o circuito) por meio das variáveis de saída e de entrada
Passo 2
Aqui podemos atribuir valores aleatórios para os componentes. Escolhemos os seguintes valores.
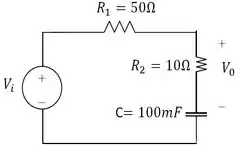
Passo 3
O passo seguinte para determinar a função de transferência é passar todos os componentes no circuito para suas respectivas impedâncias
Uma vez que a impedância do resistor não varia com a frequência
O capacitor por sua vez tem sua impedância em função da frequência. Para evitar trabalhar com números complexos vamos substituir por s.
Logo o circuito será
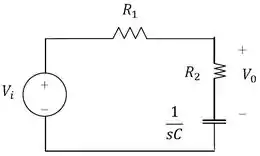
Passo 4
As variáveis de entrada e saída são respectivamente e . Será a queda sobre o resistor e sobre o capacitor
E será
Passo 5
Logo a função de transferência será
Dessa forma a função de transferência será
Resposta
A função de transferência para o problema proposto é