Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 2

Considere a Figura 8.63 e elabore um problema para ajudar outros estudantes a entenderem melhor como determinar os valores inicial e final.

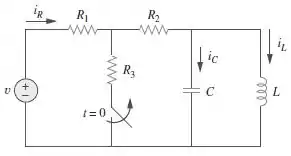
Passo 1

Podemos elaborar o problema de inúmeras maneiras possíveis. Mas vamos utilizar este exemplo.

Para o circuito da Figura abaixo, determine:

(a) i ( 0 + ) e v ( 0 + )

(b) d i ( 0 + ) / d t e d v ( 0 + ) / d t

(c) i ( ∞ ) e v ( ∞ )

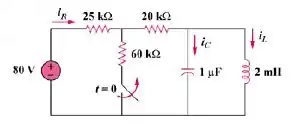
Passo 2

Primeiro vamos analisar o circuito antes da chave abrir, ou seja, t = 0 - .

Note que, o capacitor pode ser tratado como um circuito aberto, e o indutor como um curto-circuito. Assim, o circuito equivalente é,

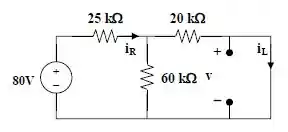
Note que, por conta do curto-circuito no indutor

v c 0 - = 0   V

Podemos fazer também o paralelo entre o resistor de 60 k e o resistor de 20k Ω , para assim utilizarmos a lei de Ohm para acharmos a corrente, portanto

60 | | 20 = 15 Ω

Logo,

i R 0 - = 80 25 + 15 = 2 m A

Se aplicarmos o princípio do divisor de corrente para descobrimos i L , temos

i L 0 - = 60 * 2 m A 60 + 20

i L 0 - = 1.5 m A

Para descobrirmos i r ( 0 + ) , basta utilizar LKV, portanto

80 = i R 0 + 25 + 20 + v C ( 0 - )

i R 0 + = 80 45 k = 1.778 m A

E como,

i R = i L + i C

Então,

1.778 = i C 0 + + 1.5

i C 0 + = 0.278   m A  

Passo 3

Para o item b) ainda continuaremos analisando o circuito quando a chave está aberta. Lembre-se que,

v L = L d i d t

Logo,

d i d t = v L L

Portanto,

d i L 0 + d t = 0

Passo 4

Similarmente, temos

i c = C d v d t

ou,

d v d t = i c C

Substituindo,

d v c 0 + d t = 278   V / s

Sabemos do passo anterior que,

80 = 45 i R + v C  

Se derivarmos, temos

0 = 45 d i R d t + d v C d t

Substituindo,

0 = 45   d i R ( 0 + ) d t + 278

d i R ( 0 + ) d t =   - 278 45

d i R ( 0 + ) d t =   - 6.1788   A / s

Como,

i R = i L + i C

Derivamos,

d i R d t   = d i L d t + d i C d t

Substituímos,

- 6.1788 = d i C 0 + d t + 0

d i C ( 0 + ) d t = - 6.1788   A / s

Passo 5

Note que o circuito tem uma alimentação, então se substituirmos o capacitor por um circuito aberto e um indutor por um circuito fechado, obtemos:

i R ∞ = i L ∞ = 80 45 k = 1.778   m A

i c ∞ = C d v ∞ / d t = 0  

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule i(t) para t0 no circuito da Figura 8.82.
Determine v(t) para t0 no circuito da Figura 8.83.
Considere o circuito da Figura 8.79. Determine vL(0+) e vc(0+).
Para o circuito da Figura 8.80, determine v(t) para t0.
Determine v(t) para t0 no circuito da Figura 8.81.