Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 15.Problemas - Ex. 20

Considere a Figura e elabore um problema para ajudar outros estudantes a entender melhor a transformada de Laplace de uma forma de onda periódica e simples.

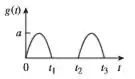
Passo 1

Antes de propormos um problema aqui, perceba que esse desenho se parece muito com a função seno:

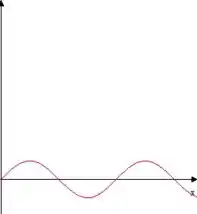
Toda função seno que não se conhece a o período T , pode ser representada assim:

sin ⁡ 2 T π t

Mas no nosso caso, pela figura...

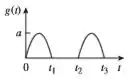
A gente sabe quem é o período T : T = t 2 = 2 t 1 ... Além disso, a nossa função seno está multiplicada por um a :

a   sin ⁡ 1 t 1 π t

SHOW! Mas ainda dá pra perceber que essa ainda não é a função g , né? Afinal, a função g tem esses intervalos de 0 ali!

A gente pode no geral falar que a função g é uma função periódica de período t 2 ...

g t = g t + t 2

E que ela vale o seguinte:

g t = a   sin ⁡ π t 1 t ,         p a r a         0 ≤ t ≤ t 1 0 ,                                                         p a r a         t 1 < t < t 2

Passo 2

Beleza, agora que a gente já sabe quem é a função g matematicamente falando, podemos definir um problema que nos ajude a entender a Transformada de Laplace de uma função periódica. Ora, acho que o problema mais apropriado para isso é:

PROBLEMA: Encontre a transformada da função periódica g t .

Pois bem, apenas a definição matemática da g não basta. Temos que tentar escrevê-la em forma de degrau! Bora?

Passo 3

Bem, perceba que antes de t = 0 , a função g é 0 e depois de t = 0 , ela passa a ser o seno, podemos escrever isso em forma de degrau:

g t = a   sin ⁡ π t 1 t u t

Mas ela não é seno para sempre, afinal em t = t 1 , ela se transforma em 0 :

g t = a   sin ⁡ π t 1 t u t - a   sin ⁡ π t 1 t u t - t 1

Isso até t = t 2 , mas depois ela se repete, afinal sabemos que g é periódica, ou seja:

g t = g t + t 2

Passo 4

Bem, de acordo com a teoria, a transformada de uma função periódica de período T h t = h t + T é...

H s = 1 1 - e - T s L h t

Então, no nosso caso, trocando h por g e T pelo período t 2 ...

G s = 1 1 - e - t 2 s L g t   →

G s = 1 1 - e - t 2 s L a   sin ⁡ π t 1 t u t - a   sin ⁡ π t 1 t u t - t 1

Ora bolas, sabemos que a transformada de função vezes o degrau é da seguinte maneira:

L x t - c u t - c = e - c s L x t

Então precisamos encontrar esse formato no seno:

sin ⁡ π t 1 t u t - t 1

Para a nossa sorte isso aí é igual a...

sin ⁡ π t 1 t - t 1 u t - t 1

Afinal, a trigonometria nos fala que sin ⁡ a - π = sin ⁡ a e no nosso caso...

sin ⁡ π t 1 t - π u t - t 1 = sin ⁡ π t 1 t u t - t 1

Saca?

Então...

G s = 1 1 - e - t 2 s L a   sin ⁡ π t 1 t u t - a   sin ⁡ π t 1 t u t - t 1   →

G s = 1 1 - e - t 2 s a L   sin ⁡ π t 1 t u t - a L   sin ⁡ π t 1 t - t 1 u t - t 1     →

Logo, pela regra do produto por um degrau a gente ganha...

G s = 1 1 - e - t 2 s a e 0 s L   sin ⁡ π t 1 t - a e - t 1 s L   sin ⁡ π t 1 t     →

Como a transformada do seno a gente conhece bem...

G s = 1 1 - e - t 2 s a π t 1 s 2 + π t 1 2 - a e - t 1 s π t 1 s 2 + π t 1 2    

Passo 5

A gente pode dar uma simplificada nisso aí e lembrar que t 2 = 2 t 1 ...

G s = 1 1 - e - 2 t 1 s a π t 1 s 2 + π t 1 2 1 - e - t 1 s       →

G s = a 1 - e - t 1 s 1 - e - 2 t 1 s π t 1 s 2 + π 2 t 1 2         →

G s = a 1 - e - t 1 s 1 - e - 2 t 1 s π t 1 s 2 t 1 2 + π 2 t 1 2         →

G s = a π t 1 1 - e - t 1 s 1 - e - 2 t 1 s 1 s 2 t 1 2 + π 2  

Prontinho! Essa é a transformada da função periódica g e é nesse mesmo esquema que se resolve a transformada de funções periódicas.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro